
| 出租天數 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 車輛數 | 5 | 10 | 30 | 35 | 15 | 3 | 2 |
| 出租天數 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 車輛數 | 14 | 20 | 20 | 16 | 15 | 10 | 5 |
分析 (I)設“事件Ai表示一臺A型挖掘機在一周內出租天數恰好為i天”,“事件Bj表示一臺B型挖掘機在一周內出租天數恰好為j天”,其i,j=1,2,…,7.則該公司一臺A型挖掘機,一臺B型挖掘機一周內合計出租天數恰好為4天的概率為P(A1B3+A2B2+A3B1)=P(A1B3)+P(A2B2)+P(A3B1)=P(A1)P(B3)+P(A2)P(B2)+P(A3)P(B1),代入概率計算即可得出.
(II)利用頻率可得概率,分別得出X,Y的分布列,即可得出數學期望.
解答 解:(I)設“事件Ai表示一臺A型挖掘機在一周內出租天數恰好為i天”,
“事件Bj表示一臺B型挖掘機在一周內出租天數恰好為j天”,其i,j=1,2,…,7.則該公司一臺A型挖掘機,一臺B型挖掘機一周內合計出租天數恰好為4天的概率為P(A1B3+A2B2+A3B1)=P(A1B3)+P(A2B2)+P(A3B1)=P(A1)P(B3)+P(A2)P(B2)+P(A3)P(B1)=$\frac{5}{100}×\frac{20}{100}$+$\frac{10}{100}×\frac{20}{100}$+$\frac{30}{100}×\frac{14}{100}$=$\frac{9}{125}$.
所以該公司一臺A型車,一臺B型車一周內合計出租天數恰好為4天的概率為$\frac{9}{125}$.
(Ⅱ)設X為A型挖掘機出租的天數,則X的分布列為
| X | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P | 0.05 | 0.10 | 0.30 | 0.35 | 0.15 | 0.03 | 0.02 |
| Y | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P | 0.14 | 0.20 | 0.20 | 0.16 | 0.15 | 0.10 | 0.05 |
點評 本題考查了頻率與概率的關系、隨機變量的分布列與數學期望,考查了推理能力與計算能力,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | [1,+∞) | B. | (0,1] | C. | [$\frac{1}{2}$,+∞) | D. | (0,$\frac{1}{2}$] |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
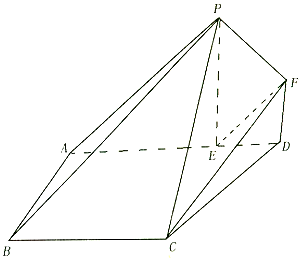 如圖,在四邊形ABCD中,∠BAD=90°,AD∥BC,PE⊥平面ABCD,E在AD上,FD∥PE,BC=AE=PE,DE=DF=$\frac{1}{2}$BC.
如圖,在四邊形ABCD中,∠BAD=90°,AD∥BC,PE⊥平面ABCD,E在AD上,FD∥PE,BC=AE=PE,DE=DF=$\frac{1}{2}$BC.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
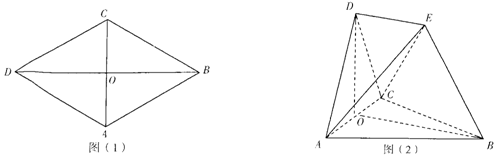
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com