某房地產開發公司計劃在一樓區內建造一個長方形公園ABCD，公園由形狀為長方形A1B1C1D1的休閑區和環公園人行道(陰影部分)組成．已知休閑區A1B1C1D1的面積為4000平方米，人行道的寬分別為4米和10米(如圖所示)．
(1)若設休閑區的長和寬的比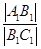
＝x(x>1)，求公園ABCD所占面積S關于x的函數S(x)的解析式；
(2)要使公園所占面積最小，則休閑區A1B1C1D1的長和寬該如何設計？
全能測控期末小狀元系列答案科目：高中數學 來源： 題型：解答題
已知定點F(0，1)和直線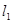
：y＝－1，過定點F與直線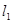相切的動圓圓心為點C.
(1)求動點C的軌跡方程；
(2)過點F的直線
交動點C的軌跡于兩點P、Q，交直線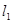于點R，求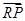
·
的最小值；
(3)過點F且與垂直的直線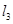
交動點C的軌跡于兩點R、T，問四邊形PRQT的面積是否存在最小值？若存在，求出這個最小值；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
為了降低能源損耗，某體育館的外墻需要建造隔熱層．體育館要建造可使用20年的隔熱層，每厘米厚的隔熱層建造成本為6萬元．該建筑物每年的能源消耗費用C（單位：萬元）與隔熱層厚度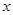
（單位：cm）滿足關系：
(
，
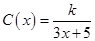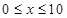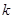為常數)，若不建隔熱層，每年能源消耗費用為8萬元．設
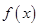為隔熱層建造費用與20年的能源消耗費用之和．
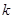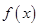（1）求的值及的表達式；
（2）隔熱層修建多厚時，總費用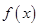達到最小？并求最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
某工廠建一個長方形無蓋蓄水池，其容積為4800m3,深度為3m。如果池底每1 m2的造價為150元，池壁每1 m2的造價為120元，怎么設計水池能使造價最低？最低造價多少元？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
(2
＋
)＋4160(x>1)．
,且
,求
及
的最小值.
.
，且
，證明不等式：
均為正實數，且
，則
的最小值為 ．
的值域是