
【題目】某公司計劃購買1臺機器,該種機器使用三年后即被淘汰.在購進機器時,可以一次性額外購買![]() 次維修,每次維修費用300元,另外實際維修一次還需向維修人員支付上門服務費80元.在機器使用期間,如果維修次數超過購買的
次維修,每次維修費用300元,另外實際維修一次還需向維修人員支付上門服務費80元.在機器使用期間,如果維修次數超過購買的![]() 次時,則超出的維修次數,每次只需支付維修費用700元,無需支付上門服務費.需決策在購買機器時應同時一次性購買幾次維修,為此搜集并整理了100臺這種機器在三年使用期內的維修次數,得到下面統計表:
次時,則超出的維修次數,每次只需支付維修費用700元,無需支付上門服務費.需決策在購買機器時應同時一次性購買幾次維修,為此搜集并整理了100臺這種機器在三年使用期內的維修次數,得到下面統計表:
維修次數 | 6 | 7 | 8 | 9 | 10 |
頻數 | 10 | 20 | 30 | 30 | 10 |
記![]() 表示1臺機器在三年使用期內的維修次數,
表示1臺機器在三年使用期內的維修次數,![]() 表示1臺機器維修所需的總費用(單位:元).
表示1臺機器維修所需的總費用(單位:元).
(1)若![]() ,求
,求![]() 與
與![]() 的函數解析式;
的函數解析式;
(2)假設這100臺機器在購機的同時每臺都購買8次維修,或每臺都購買9次維修,分別計算這100臺機器在維修上所需總費用的平均數,并以此作為決策依據,購買1臺機器的同時應購買8次還是9次維修?
【答案】(1) ![]() ,
,![]() .(2)
.(2) ![]() ;
;![]() ;購買1臺機器的同時應購買8次維修服務.
;購買1臺機器的同時應購買8次維修服務.
【解析】
(1)由題意結合題意將原問題轉化為分段函數求解析式的問題即可確定函數的解析式;
(2)由題意分別求得購買8次維修服務和購買9次維修服務所需費用的平均數,比較兩個平均數的大小即可給出決策.
(1)由題意得,當![]() 時,
時,![]() ;
;
當![]() 時,
時,![]() ,
,
即![]() ,
,![]() .
.
(2)若每臺都購買8次維修服務,則有下表:
維修次數 | 6 | 7 | 8 | 9 | 10 |
頻數 | 10 | 20 | 30 | 30 | 10 |
費用 | 2880 | 2960 | 3040 | 3740 | 4440 |
此時,這100臺機器在維修上所需費用的平均數為
![]()
![]() (元).
(元).
若每臺都購買9次維修服務,則有下表:
維修次數 | 6 | 7 | 8 | 9 | 10 |
頻數 | 10 | 20 | 30 | 30 | 10 |
費用 | 3180 | 3260 | 3340 | 3420 | 4120 |
此時,這100臺機器在維修上所需費用的平均數為
![]()
![]() (元).
(元).
因為![]() ,購買1臺機器的同時應購買8次維修服務.
,購買1臺機器的同時應購買8次維修服務.


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案科目:高中數學 來源: 題型:
【題目】為了研究高中學生對鄉村音樂的態度(喜歡和不喜歡兩種態度)與性別的關系,運用2×2列聯表進行獨立性檢驗,經計算K2=8.01,附表如下:
P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
參照附表,得到的正確的結論是( )
A. 有99%以上的把握認為“喜歡鄉村音樂與性別有關”
B. 有99%以上的把握認為“喜歡鄉村音樂與性別無關”
C. 在犯錯誤的概率不超過0.1%的前提下,認為“喜歡鄉村音樂與性別有關”
D. 在犯錯誤的概率不超過0.1%的前提下,認為“喜歡鄉村音樂與性別無關”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某書店銷售剛剛上市的某高二數學單元測試卷,按事先擬定的價格進行5天試銷,每種單價試銷1天,得到如下數據:
單價x/元 | 18 | 19 | 20 | 21 | 22 |
銷量y/冊 | 61 | 56 | 50 | 48 | 45 |
(1)求試銷![]() 天的銷量的方差和
天的銷量的方差和![]() 關于
關于![]() 的回歸直線方程;
的回歸直線方程;
附: 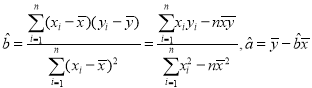 .
.
(2)預計以后的銷售中,銷量與單價服從上題中的回歸直線方程,已知每冊單元測試卷的成本是10元,為了獲得最大利潤,該單元測試卷的單價應定為多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若直線![]() 與曲線
與曲線![]() 滿足下列兩個條件:①直線
滿足下列兩個條件:①直線![]() 在點
在點![]() 處與曲線
處與曲線![]() 相切;②曲線
相切;②曲線![]() 在點
在點![]() 附近位于直線
附近位于直線![]() 的兩側,則稱直線
的兩側,則稱直線![]() 在點
在點![]() 處“切過”曲線
處“切過”曲線![]() .則下列結論正確的是( )
.則下列結論正確的是( )
A.直線![]() 在點
在點![]() 處“切過”曲線
處“切過”曲線![]()
B.直線![]() 在點
在點![]() 處“切過”曲線
處“切過”曲線![]()
C.直線![]() 在點
在點![]() 處“切過”曲線
處“切過”曲線![]()
D.直線![]() 在點
在點![]() 處“切過”曲線
處“切過”曲線![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com