
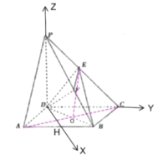
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為菱形,
為菱形,![]() ,側棱
,側棱![]() 底面
底面![]() ,
,![]() ,點
,點![]() 為
為![]() 的中點,作
的中點,作![]() ,交
,交![]() 于點
于點![]() .
.
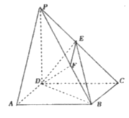
(1)求證:![]() 平面
平面![]() ;
;
(2)求證:![]() ;
;
(3)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)見解析(2)見解析 (3)![]()
【解析】
(1)連接![]() 交
交![]() 于
于![]() ,連接
,連接![]() ,根據中位線定理證明
,根據中位線定理證明![]() ,即可證得
,即可證得![]() 平面
平面![]() .
.
(2)先證![]() 平面
平面![]() .又∵
.又∵![]() 平面
平面![]() ,則
,則![]() .
.
(3)建立空間直角坐標系,列出各點的坐標表示,求出平面![]() 的法向量為
的法向量為![]() ,又因
,又因![]() 平面
平面![]() ,所以
,所以![]() 為平面
為平面![]() 的一條法向量,利用余弦公式求解即可得出二面角
的一條法向量,利用余弦公式求解即可得出二面角![]() 的余弦值.
的余弦值.
解:(1)證明:連接![]() 交
交![]() 于
于![]() ,連接
,連接![]() .
.
因為![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點,所以
的中點,所以![]() 為
為![]() 的中位線
的中位線
∴![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]()
(2)在![]() 中,
中,![]() ,點
,點![]() 為
為![]() 的中點,
的中點,
∴ ,則
,則![]() 平面
平面![]() .
.
又∵![]() 平面
平面![]() ,則
,則![]() .
.
(3)取![]() 中點
中點![]() ,連接
,連接![]() .
.
依題意可得![]() 為等邊三角形,∴
為等邊三角形,∴![]() ,
,![]()
又因為![]() 底面
底面![]() ,
,![]() ,
,![]() 平面
平面![]()
則![]() ,
,![]()
建立以![]() 為坐標原點,如圖所示坐標系,則有:
為坐標原點,如圖所示坐標系,則有:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,設平面
,設平面![]() 的法向量為
的法向量為![]() ,
,
則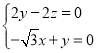
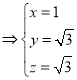 ,∴
,∴![]()
∵![]() 平面
平面![]() ,所以
,所以![]() 為平面
為平面![]() 的一條法向量,且
的一條法向量,且![]()
∴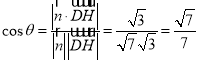


科目:高中數學 來源: 題型:
【題目】蘋果是人們日常生活中常見的營養型水果.某地水果批發市場銷售來自5個不同產地的富士蘋果,各產地的包裝規格相同,它們的批發價格(元/箱)和市場份額如下:
產地 |
|
|
|
|
|
批發價格 |
|
|
|
|
|
市場份額 |
|
|
|
|
|
市場份額亦稱“市場占有率”.指某一產品的銷售量在市場同類產品中所占比重.
(1)從該地批發市場銷售的富士蘋果中隨機抽取一箱,求該箱蘋果價格低于![]() 元的概率;
元的概率;
(2)按市場份額進行分層抽樣,隨機抽取![]() 箱富士蘋果進行檢驗,
箱富士蘋果進行檢驗,
①從產地![]() 共抽取
共抽取![]() 箱,求
箱,求![]() 的值;
的值;
②從這![]() 箱蘋果中隨機抽取兩箱進行等級檢驗,求兩箱產地不同的概率;
箱蘋果中隨機抽取兩箱進行等級檢驗,求兩箱產地不同的概率;
(3)由于受種植規模和蘋果品質的影響,預計明年產地![]() 的市場份額將增加
的市場份額將增加![]() ,產地
,產地![]() 的市場份額將減少
的市場份額將減少![]() ,其它產地的市場份額不變,蘋果銷售價格也不變(不考慮其它因素).設今年蘋果的平均批發價為每箱
,其它產地的市場份額不變,蘋果銷售價格也不變(不考慮其它因素).設今年蘋果的平均批發價為每箱![]() 元,明年蘋果的平均批發價為每箱
元,明年蘋果的平均批發價為每箱![]() 元,比較
元,比較![]() 的大小.(只需寫出結論)
的大小.(只需寫出結論)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的左右焦點分別為
的左右焦點分別為![]() 、
、![]() ,橢圓的離心率為
,橢圓的離心率為![]() ,
,![]() 為橢圓上任意一點,
為橢圓上任意一點,![]() 的最大面積為
的最大面積為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過![]() 的直線
的直線![]() 與橢圓交于
與橢圓交于![]() 、
、![]() 兩點,連接
兩點,連接![]() 、
、![]() ,若
,若![]() 的內切圓面積為
的內切圓面積為![]() ,則求直線
,則求直線![]() 方程.
方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列五個命題:
①凈![]() 三種個體按
三種個體按![]() 的比例分層抽樣調查,如果抽取的
的比例分層抽樣調查,如果抽取的![]() 個體為9個,則樣本容易為30;②一組數據1、2、3、4、5的平均數、眾數、中位數相同;③甲組數據的方差為5,乙組數據為5、6、9、10、5,那么這兩組數據中較穩定的是甲;④已知具有線性相關關系的兩個變量滿足的回歸直線方程為
個體為9個,則樣本容易為30;②一組數據1、2、3、4、5的平均數、眾數、中位數相同;③甲組數據的方差為5,乙組數據為5、6、9、10、5,那么這兩組數據中較穩定的是甲;④已知具有線性相關關系的兩個變量滿足的回歸直線方程為![]() .則
.則![]() 每增加1個單位,
每增加1個單位,![]() 平均減少2個單位;⑤統計的10個樣本數據為125,120,122,105,130,114,116,95,120,134,則樣本數據落在
平均減少2個單位;⑤統計的10個樣本數據為125,120,122,105,130,114,116,95,120,134,則樣本數據落在![]() 內的頻率為0.4其中真命題為( )
內的頻率為0.4其中真命題為( )
A. ①②④B. ②④⑤C. ②③④D. ③④⑤
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四邊形
,四邊形![]() 為矩形,
為矩形,![]() .
.
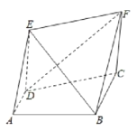
(1)求證:平面![]() 平面
平面![]() ;
;
(2)在線段![]() 上是否存在點
上是否存在點![]() ,使得直線
,使得直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,若存在,求出線段
,若存在,求出線段![]() 的長,若不存在,請說明理由.
的長,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在以![]() 為頂點,母線長為
為頂點,母線長為![]() 的圓錐中,底面圓
的圓錐中,底面圓![]() 的直徑
的直徑![]() 長為2,
長為2,![]() 是圓
是圓![]() 所在平面內一點,且
所在平面內一點,且![]() 是圓
是圓![]() 的切線,連接
的切線,連接![]() 交圓
交圓![]() 于點
于點![]() ,連接
,連接![]() ,
,![]() .
.
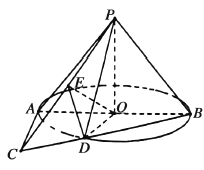
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中點,連接
的中點,連接![]() ,
,![]() ,當二面角
,當二面角![]() 的大小為
的大小為![]() 時,求平面
時,求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司計劃購買1臺機器,該種機器使用三年后即被淘汰.在購進機器時,可以一次性額外購買![]() 次維修,每次維修費用300元,另外實際維修一次還需向維修人員支付上門服務費80元.在機器使用期間,如果維修次數超過購買的
次維修,每次維修費用300元,另外實際維修一次還需向維修人員支付上門服務費80元.在機器使用期間,如果維修次數超過購買的![]() 次時,則超出的維修次數,每次只需支付維修費用700元,無需支付上門服務費.需決策在購買機器時應同時一次性購買幾次維修,為此搜集并整理了100臺這種機器在三年使用期內的維修次數,得到下面統計表:
次時,則超出的維修次數,每次只需支付維修費用700元,無需支付上門服務費.需決策在購買機器時應同時一次性購買幾次維修,為此搜集并整理了100臺這種機器在三年使用期內的維修次數,得到下面統計表:
維修次數 | 6 | 7 | 8 | 9 | 10 |
頻數 | 10 | 20 | 30 | 30 | 10 |
記![]() 表示1臺機器在三年使用期內的維修次數,
表示1臺機器在三年使用期內的維修次數,![]() 表示1臺機器維修所需的總費用(單位:元).
表示1臺機器維修所需的總費用(單位:元).
(1)若![]() ,求
,求![]() 與
與![]() 的函數解析式;
的函數解析式;
(2)假設這100臺機器在購機的同時每臺都購買8次維修,或每臺都購買9次維修,分別計算這100臺機器在維修上所需總費用的平均數,并以此作為決策依據,購買1臺機器的同時應購買8次還是9次維修?
查看答案和解析>>
科目:高中數學 來源: 題型:
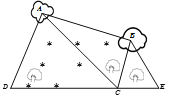
【題目】如圖,為了測量某濕地![]() 兩點間的距離,觀察者找到在同一直線上的三點
兩點間的距離,觀察者找到在同一直線上的三點![]() .從
.從![]() 點測得
點測得![]() ,從
,從![]() 點測得
點測得![]() ,
,![]() ,從
,從![]() 點測得
點測得![]() .若測得
.若測得![]() ,
,![]() (單位:百米),則
(單位:百米),則![]() 兩點的距離為( )
兩點的距離為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com