
分析 (1)根據函數f(x)+g(x)的定義域關于原點對稱,且滿足 f(-x)+g(-x)=f(x)+g(x),可得函數f(x)+g(x)為偶函數.
(2)令x=$\sqrt{3}$,求得f(x)+g(x)=loga(4-x2) 的值.
解答 解:(1)由題意可得f(x)+g(x)的定義域為(-2,2),f(x)+g(x)=loga(4-x2),
∴f(-x)+g(-x)=loga(4-x2)=f(x)+g(x),故函數f(x)+g(x)為偶函數.
(2)f($\sqrt{3}$)+g($\sqrt{3}$)=loga(4-3)=0.
點評 本題主要考查函數的奇偶性的判斷方法,求函數的值,屬于基礎題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | y=-2x+1 | B. | y=x2-2 | C. | y=$\frac{1}{x}$ | D. | y=($\frac{1}{2}$)x |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
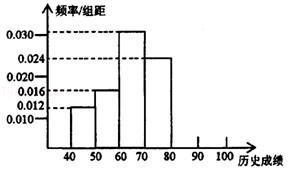 某校高一學生共有500人,為了了解學生的歷史學習情況,隨機抽取了50名學生,對他們一年來4次考試的歷史平均成績進行統(tǒng)計,得到頻率分布直方圖如圖所示,后三組頻數成等比數列.
某校高一學生共有500人,為了了解學生的歷史學習情況,隨機抽取了50名學生,對他們一年來4次考試的歷史平均成績進行統(tǒng)計,得到頻率分布直方圖如圖所示,后三組頻數成等比數列.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com