
如圖,三棱柱 中,側面
中,側面 是邊長為2的菱形,且
是邊長為2的菱形,且 ,
, ,四棱錐
,四棱錐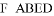 的體積為2,點
的體積為2,點 在平面
在平面 內的正投影為
內的正投影為 ,且
,且 在
在 上點
上點 是線段
是線段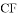 上,且
上,且 .
.

(1)證明:直線 平面
平面 ;
;
(2)求二面角 的余弦值.
的余弦值.
 優加精卷系列答案
優加精卷系列答案科目:高中數學 來源:2016-2017學年云南省高二上學期期末考試數學(理)試卷(解析版) 題型:解答題
已知焦點在 軸上的橢圓
軸上的橢圓 的中心是原點
的中心是原點 ,離心率為雙曲線
,離心率為雙曲線 離心率的一半,直線
離心率的一半,直線 被橢圓
被橢圓 截得的線段長為
截得的線段長為 .直線
.直線 :
:  與
與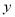 軸交于點
軸交于點 ,與橢圓
,與橢圓 交于
交于 兩個相異點,且
兩個相異點,且 .
.
(1)求橢圓 的方程;
的方程;
(2)是否存在實數 ,使
,使 ?若存在,求
?若存在,求 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源:2017屆安徽省宿州市高三第一次教學質量檢測(期末)理數試卷(解析版) 題型:選擇題
下邊程序框圖的算法思路源于我國古代數學名著《九章算術》中的“更相減損術”.執行該程序框圖,若輸入 ,
, 的值分別為
的值分別為 ,
, ,則輸出的
,則輸出的 的值為( )
的值為( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:高中數學 來源:2016-2017學年安徽省六安市高一上學期周末作業(十三)數學試卷(解析版) 題型:選擇題
直線 繞差其上一點
繞差其上一點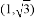 沿逆時針方向旋轉15°,則旋轉后得到的直線
沿逆時針方向旋轉15°,則旋轉后得到的直線 的方程為( )
的方程為( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:高中數學 來源:2017屆河北省石家莊市高三第二次質量檢測數學(理)試卷(解析版) 題型:解答題
選修4-5:不等式選講
設函數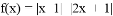 的最大值為
的最大值為 .
.
(1)作出函數 的圖象;
的圖象;
(2)若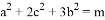 ,求
,求 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源:2017屆河北省石家莊市高三第二次質量檢測數學(理)試卷(解析版) 題型:選擇題
李冶(1192-1279),真定欒城(今屬河北石家莊市)人,金元時期的數學家、詩人、晚年在封龍山隱居
講學,數學著作多部,其中《益古演段》主要研究平面圖形問題:求圓的直徑,正方形的邊長等,其中一問:現有正方形方田一塊,內部有一個圓形水池,其中水池的邊緣與方田四邊之間的面積為 畝,若方田的四邊到水池的最近距離均為二十步,則圓池直徑和方田的邊長分別是(注:
畝,若方田的四邊到水池的最近距離均為二十步,則圓池直徑和方田的邊長分別是(注:  平方步為
平方步為 畝,圓周率按
畝,圓周率按 近似計算)
近似計算)
A.  步、
步、 步 B.
步 B.  步、
步、 步 C.
步 C.  步、
步、 步 D.
步 D.  步、
步、 步
步
查看答案和解析>>
科目:高中數學 來源:2017屆貴州省貴陽市高三2月適應性考試(一)數學理試卷(解析版) 題型:選擇題
已知
是函數
在
上的所有零點之和,則
的值為( )
A. 4 B. 6 C. 8 D. 10
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com