
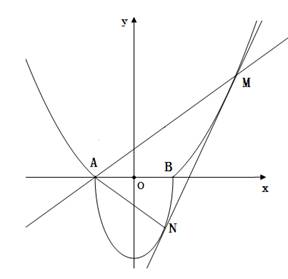
 如圖,
如圖,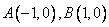 ,過曲線
,過曲線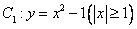 上一點(diǎn)
上一點(diǎn)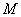 的切線
的切線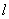 ,與曲線
,與曲線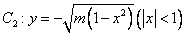 也相切于點(diǎn)
也相切于點(diǎn)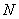 .記點(diǎn)
.記點(diǎn)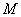 的橫坐標(biāo)為
的橫坐標(biāo)為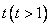 .
.
(Ⅰ)當(dāng)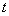 =2時,求實數(shù)
=2時,求實數(shù)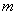 的值和點(diǎn)
的值和點(diǎn)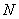 的坐標(biāo);
的坐標(biāo);
(Ⅱ)當(dāng)實數(shù)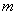 取何值時,
取何值時,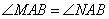 ?
?
并求此時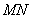 所在直線的方程.
所在直線的方程.
解:(1)切線l:y-3=4(x-2),即y=4x-分
代入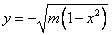 ,
,
化簡并整理得
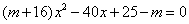 (*)
(*)
由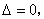
得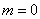 ,或m=9.-----------------------------------------------------------------------4分
,或m=9.-----------------------------------------------------------------------4分
若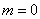 ,代入(*)式得xN=
,代入(*)式得xN=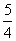 ,與已知
,與已知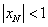 矛盾;------------------5分
矛盾;------------------5分
若m=9,代入(*)式得xN=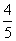 滿足條件,且yN=-
滿足條件,且yN=-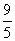 ,
,
綜上,m=9,點(diǎn)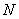 的坐標(biāo)為(
的坐標(biāo)為(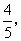 -
-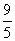 ).-------------------------------------------6分
).-------------------------------------------6分
(2)切線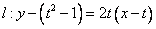 ,即
,即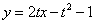 ,----------------------------8分
,----------------------------8分
代入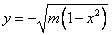 ,
,
化簡并整理得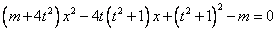 ,(*)
,(*)
由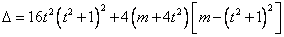
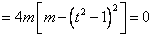
得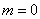 或
或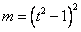 .-------------------------------------------------------------10分
.-------------------------------------------------------------10分
若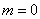 ,代入(*)式得
,代入(*)式得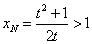 ,與已知
,與已知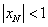 矛盾;
矛盾;
若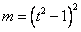 ,代入(*)式得
,代入(*)式得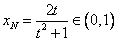 滿足條件,
滿足條件,
且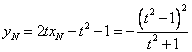 ,
,
因此,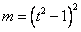 ,點(diǎn)
,點(diǎn)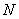 的坐標(biāo)為
的坐標(biāo)為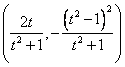 。-------------------12分
。-------------------12分
因為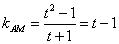 ,
, ,
,
若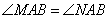 ,則
,則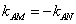 ,即
,即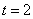 ,此時
,此時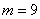 ,
,
故當(dāng)實數(shù)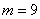 時,
時,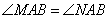 。
--------------------14分
。
--------------------14分
此時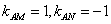 ,
,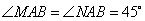 ,
,
易得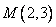 ,
,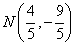 ,
,
此時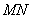 所在直線的方程為
所在直線的方程為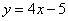 .----------------------------------------------15分
.----------------------------------------------15分



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:2010-2011學(xué)年江西省上饒市四校高三第二次聯(lián)考數(shù)學(xué)理卷 題型:解答題
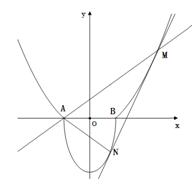
.如圖,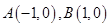 ,過曲線
,過曲線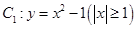 上 一點(diǎn)
上 一點(diǎn)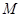 的切線
的切線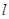 ,與曲線
,與曲線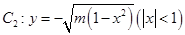 也相切于點(diǎn)
也相切于點(diǎn)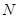 ,記點(diǎn)
,記點(diǎn)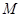 的橫坐標(biāo)為
的橫坐標(biāo)為 。
。
(1)用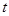 表示
表示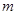 的值和點(diǎn)
的值和點(diǎn)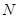 的坐標(biāo);
的坐標(biāo);
(2)當(dāng)實數(shù)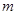 取何值時,
取何值時,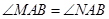 ?
?
并求此時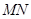 所在直線的方程。
所在直線的方程。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
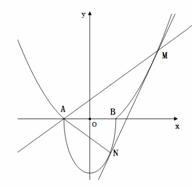
如圖,![]() ,過曲線
,過曲線![]() 上 一點(diǎn)
上 一點(diǎn)![]() 的切線
的切線![]() ,與曲線
,與曲線![]() 也相切于點(diǎn)
也相切于點(diǎn)![]() ,記點(diǎn)
,記點(diǎn)![]() 的橫坐標(biāo)為
的橫坐標(biāo)為![]() 。
。
(1)用![]() 表示
表示![]() 的值和點(diǎn)
的值和點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(2)當(dāng)實數(shù)![]() 取何值時,
取何值時,![]() ?并求此時
?并求此時![]() 所在直線的方程。
所在直線的方程。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
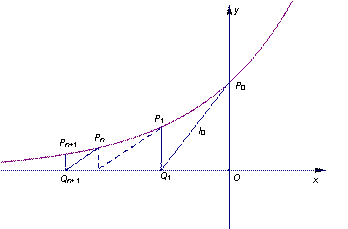
(本小題滿分14分)如圖5,過曲線![]() :
:![]() 上一點(diǎn)
上一點(diǎn)![]() 作曲線
作曲線![]() 的切線
的切線![]() 交
交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,又過
,又過![]() 作
作 ![]() 軸的垂線交曲線
軸的垂線交曲線![]() 于點(diǎn)
于點(diǎn)![]() ,然后再過
,然后再過![]() 作曲線
作曲線![]() 的切線
的切線![]() 交
交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,又過
,又過![]() 作
作![]() 軸的垂線交曲線
軸的垂線交曲線![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() ,以此類推,過點(diǎn)
,以此類推,過點(diǎn)![]() 的切線
的切線![]() 與
與![]() 軸相交于點(diǎn)
軸相交于點(diǎn)![]() ,再過點(diǎn)
,再過點(diǎn)![]() 作
作![]() 軸的垂線交曲線
軸的垂線交曲線![]() 于點(diǎn)
于點(diǎn)![]() (
(![]() N
N![]() ).
).
(1) 求![]() 、
、![]() 及數(shù)列
及數(shù)列![]() 的通項公式;
的通項公式;
(2) 設(shè)曲線![]() 與切線
與切線![]() 及直線
及直線![]() 所圍成的圖形面積為
所圍成的圖形面積為![]() ,求
,求![]() 的表達(dá)式;
的表達(dá)式;
 (3) 在滿足(2)的條件下, 若數(shù)列
(3) 在滿足(2)的條件下, 若數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,求證:
,求證:![]()
![]() N
N![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:湖北省襄樊五中2010年高三年級五月適應(yīng)性考試(理) 題型:解答題
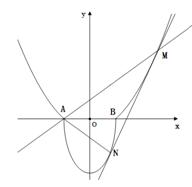
如圖,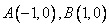 ,過曲線
,過曲線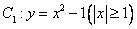 上一點(diǎn)
上一點(diǎn)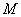 的切線
的切線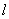 ,與曲線
,與曲線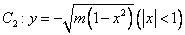 也相切于點(diǎn)
也相切于點(diǎn)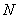 ,記點(diǎn)
,記點(diǎn)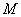 的橫坐標(biāo)為
的橫坐標(biāo)為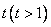 。
。
 (1)用
(1)用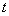 表示切線
表示切線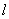 的方程;
的方程;
(2)用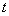 表示
表示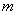 的值和點(diǎn)
的值和點(diǎn)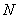 的坐標(biāo);
的坐標(biāo);
(3)當(dāng)實數(shù)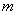 取何值時,
取何值時,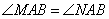 ?
?
并求此時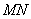 所在直線的方程。
所在直線的方程。
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com