
分析 (1)利用同角三角函數關系式,消去t可得圓C的普通方程,利用余弦的兩角和與差打開,x=ρcosθ,y=ρsinθ可得直線L的直角坐標方程;
(2)將A,B兩點的極坐標化為直角坐標.求出AB的距離,利用參數坐標設出點P.可得△PAB面積的關系式,求最大值即可.
解答 解:(1)圓C的參數方程為$\left\{\begin{array}{l}x=1+\sqrt{2}cost\\ y=-1+\sqrt{2}sint\end{array}\right.$,(t為參數),可得:$\left\{\begin{array}{l}{x-1=\sqrt{2}cost}\\{1+y=\sqrt{2}sint}\end{array}\right.$,得$\left\{\begin{array}{l}{(x-1)^{2}=2co{s}^{2}t}\\{(y+1)^{2}=2si{n}^{2}t}\end{array}\right.$
可得:(x-1)2+(y+1)2=2,
即圓C的普通方程為:(x-1)2+(y+1)2=2,
直線l的極坐標方程為$ρcos({θ+\frac{π}{4}})=-\frac{{\sqrt{2}}}{2}$,
可得:$ρcosθ×cos\frac{π}{4}-ρsinθ×sin\frac{π}{4}=-\frac{\sqrt{2}}{2}$,得$\frac{\sqrt{2}}{2}ρcosθ-\frac{\sqrt{2}}{2}ρsinθ+\frac{\sqrt{2}}{2}=0$
由x=ρcosθ,y=ρsinθ,可得:x-y+1=0.
∴直線L的直角坐標方程為x-y+1=0.
(2)A,B兩點的極坐標為$({1,\frac{π}{2}}),({1,π})$.
化簡直角坐標為A(0,1),B(-1,0),可得A,B在直線直線l上.|AB|=$\sqrt{2}$.
點P是圓C上,設P(1$+\sqrt{2}cost$,$-1+\sqrt{2}sint$),
則P到直線l的距離d=$\frac{|1+\sqrt{2}cost+1-\sqrt{2}sint+1|}{\sqrt{2}}=\frac{|3+2cos(t+\frac{π}{4})|}{\sqrt{2}}$
∴$p9vv5xb5_{max}=\frac{5}{\sqrt{2}}=\frac{5\sqrt{2}}{2}$.
∴△PAB面積的最大值為:$S=\frac{1}{2}|AB|×p9vv5xb5_{max}=\frac{1}{2}×\sqrt{2}×\frac{5\sqrt{2}}{2}=\frac{5}{2}$.
點評 本題考查了參數方程化為普通方程,極坐標化為直角坐標的問題.點到直線的距離公式求最值問題.屬于中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
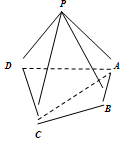 如圖,在四棱錐P-ABCD中,平面PAD⊥平面ABCD,△ADP是等腰直角三角形,∠APD是直角,AB⊥AD,AB=1,$AD=2,AC=CD=\sqrt{5}$.
如圖,在四棱錐P-ABCD中,平面PAD⊥平面ABCD,△ADP是等腰直角三角形,∠APD是直角,AB⊥AD,AB=1,$AD=2,AC=CD=\sqrt{5}$.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 函數f(x)+x2是奇函數 | B. | 函數f(x)+|x|是偶函數 | ||
| C. | 函數x2f(x)是奇函數 | D. | 函數|x|f(x)是偶函數 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
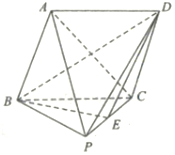 如圖,在四棱錐P-ABCD中,底面ABCD是菱形,側面PBC是直角三角形,∠PCB=90°,點E是PC的中點,且平面PBC⊥平面ABCD.
如圖,在四棱錐P-ABCD中,底面ABCD是菱形,側面PBC是直角三角形,∠PCB=90°,點E是PC的中點,且平面PBC⊥平面ABCD.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 資源 產品 | 資金(萬元) | 場地(平方米) |
| A | 2 | 100 |
| B | 35 | 50 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com