
【題目】已知:f(x)=lg(ax﹣bx)(a>1>b>0).
(1)求f(x)的定義域;
(2)判斷f(x)在其定義域內的單調性.
【答案】
(1)解:要使函數有意義,則ax﹣bx>0,∴ ,
∵ ,∴x>0,∴f(x)的定義域為(0,+∞).
(2)解:設x2>x1>0,∵a>1>b>0,
∴ , ,則 ,
∴ ,∴ 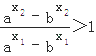 .
.
∵函數y=lgx在定義域上是增函數,
∴f(x2)﹣f(x1)>0,即f(x2)>f(x1),
∴f(x)在(0,+∞)是增函數.
【解析】(1)由對數的真數大于零得,ax﹣bx>0,再由a>1>b>0和指數函數的性質,求出不等式解集即函數的定義域;(2)先在定義域任取兩個自變量,即x2>x1>0,利用指數函數的性質比較對應真數的大小,再根據y=lgx在定義域上是增函數,得出f(x2)與f(x1)的大小,判斷出此函數的單調性;
【考點精析】本題主要考查了函數單調性的性質的相關知識點,需要掌握函數的單調區間只能是其定義域的子區間 ,不能把單調性相同的區間和在一起寫成其并集才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】已知橢圓的左焦點為F1有一小球A 從F1處以速度v開始沿直線運動,經橢圓壁反射(無論經過幾次反射速度大小始終保持不變,小球半徑忽略不計),若小球第一次回到F1時,它所用的最長時間是最短時間的5倍,則橢圓的離心率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量 ![]() ,將函數
,將函數 ![]() 的圖象按向量
的圖象按向量 ![]() 平移后得到函數g(x)的圖象.
平移后得到函數g(x)的圖象.
(1)求函數g(x)的表達式;
(2)若函數 ![]() 上的最小值為h(a),求h(a)的最大值.
上的最小值為h(a),求h(a)的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(n)=1+ ![]() ,g(n)=
,g(n)= ![]() ﹣
﹣ ![]() ,n∈N* .
,n∈N* .
(1)當n=1,2,3時,試比較f(n)與g(n)的大小關系;
(2)猜想f(n)與g(n)的大小關系,并給出證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】向量的運算常常與實數運算進行類比,下列類比推理中結論正確的是( )
A.“若ac=bc(c≠0),則a=b”類比推出“若 ![]()
![]() =
= ![]()
![]() (
( ![]() ≠
≠ ![]() ),則
),則 ![]() =
= ![]() ”
”
B.“在實數中有(a+b)c=ac+bc”類比推出“在向量中( ![]() +
+ ![]() )
) ![]() =
= ![]()
![]() +
+ ![]()
![]() ”
”
C.“在實數中有(ab)c=a(bc)”類比推出“在向量中( ![]()
![]() )
) ![]() =
= ![]() (
( ![]()
![]() )”
)”
D.“若ab=0,則a=0或b=0”類比推出“若 ![]()
![]() =0,則
=0,則 ![]() =
= ![]() 或
或 ![]() =
= ![]() ”
”
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com