
| A. | 是銳角三角形 | B. | 是直角三角形 | C. | 是鈍角三角形 | D. | 不存在 |
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
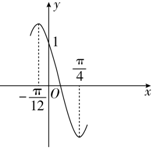 已知函數y=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分圖象如圖所示,則經過點P(φ,0),斜率為A的直線的方程為( )
已知函數y=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分圖象如圖所示,則經過點P(φ,0),斜率為A的直線的方程為( )| A. | y=$\sqrt{2}$(x-$\frac{3π}{4}$) | B. | y=$\sqrt{2}$(x-$\frac{π}{4}$) | C. | y=$\sqrt{3}$(x-$\frac{π}{3}$) | D. | y=$\sqrt{3}$(x-$\frac{2π}{3}$) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 34 | B. | 27 | C. | 25 | D. | 16 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 系統抽樣 | |
| B. | 簡單隨機抽樣 | |
| C. | 分層抽樣 | |
| D. | 先從高級職務干部中剔除1人,再用分層抽樣 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com