
分析 (1)由${2}^{{a}_{3}}$=8,$,{2}^{{a}_{5}}$=128,可得a3=3,a5=7,再利用等差數列的通項公式及其性質即可得出.
(2)${b_n}=\frac{1}{{{a_n}{a_{n+1}}}}=\frac{1}{(2n-3)(2n-1)}=\frac{1}{2}(\frac{1}{2n-3}-\frac{1}{2n-1})$,利用裂項求和方法即可得出.
解答 解:(1)由${2}^{{a}_{3}}$=8,$,{2}^{{a}_{5}}$=128,可得a3=3,a5=7,
設數列{an}的公差為d,則2d=a5-a3=4⇒d=2,
所以an=a3+(n-3)d=2n-3.
(2)因為${b_n}=\frac{1}{{{a_n}{a_{n+1}}}}=\frac{1}{(2n-3)(2n-1)}=\frac{1}{2}(\frac{1}{2n-3}-\frac{1}{2n-1})$,
所以Tn=$\frac{1}{2}[(-1-1)$+$(1-\frac{1}{3})$+$(\frac{1}{3}-\frac{1}{5})$+…+$(\frac{1}{2n-3}-\frac{1}{2n-1})]$=$\frac{1}{2}(-1-\frac{1}{2n-1})$=$\frac{n}{1-2n}$.
點評 本題考查了等差數列的通項公式與求和公式、裂項求和方法,考查了推理能力與計算能力,屬于中檔題.


 同步輕松練習系列答案
同步輕松練習系列答案 課課通課程標準思維方法與能力訓練系列答案
課課通課程標準思維方法與能力訓練系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -2 | B. | 2 | C. | 8 | D. | -8 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{{n^2}+5n}}{2}$ | B. | $\frac{{{n^2}+5n}}{4}$ | C. | $\frac{{{n^2}+3n}}{2}$ | D. | $\frac{{{n^2}+3n}}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
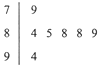 如圖是2015年日喀則市舉辦青少年運動會上,7位裁判為某武術隊員打出的分數的莖葉圖,左邊數字表示十位數字,右邊數字表示個位數字.這些數據的中位數是______,去掉一個最低分和最高分后所剩數據的平均數是( )
如圖是2015年日喀則市舉辦青少年運動會上,7位裁判為某武術隊員打出的分數的莖葉圖,左邊數字表示十位數字,右邊數字表示個位數字.這些數據的中位數是______,去掉一個最低分和最高分后所剩數據的平均數是( )| A. | 86.5; 86.7 | B. | 88; 86.7 | C. | 88;86.8 | D. | 86.5;86.8 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (2$\sqrt{2}$,+∞) | B. | (-∞,-2$\sqrt{2}$)∪(2$\sqrt{2}$,+∞) | C. | (-2$\sqrt{2}$,2)∪(2$\sqrt{2}$,+∞) | D. | (-∞,-2)∪(2,+∞) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com