
【題目】選修4-4:坐標系與參數方程
已知直線![]() 的極坐標方程是
的極坐標方程是![]() ,以極點為原點,極軸為
,以極點為原點,極軸為![]() 軸的正半軸建立極坐標系,曲線
軸的正半軸建立極坐標系,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).
為參數).
(1)寫出直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設![]() 為曲線
為曲線![]() 上任意一點,求
上任意一點,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】試題分析:(1)根據直線![]() 的極坐標方程,即可求得直線l的直角坐標公式,由橢圓C的參數方程即可求得曲線C的直角坐標方程;
的極坐標方程,即可求得直線l的直角坐標公式,由橢圓C的參數方程即可求得曲線C的直角坐標方程;
(2)由(1)可得丨x-y-4丨=丨2cosφ-sinφ-4丨,根據輔助角公式及正弦函數的性質,即可求得|x-y-4|的最小值.
試題解析:
(1)由![]() ρcosθ-ρsinθ=4,將x=ρcosθ,y=ρsinθ代入即得直線l的直角坐標方程為
ρcosθ-ρsinθ=4,將x=ρcosθ,y=ρsinθ代入即得直線l的直角坐標方程為 ![]() ;曲線
;曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數)所以
為參數)所以![]() .
.
(2)設![]() ,則丨x-y-4丨=丨2cosφ-sinφ-4丨=|
,則丨x-y-4丨=丨2cosφ-sinφ-4丨=|![]() cos(φ+α)-4丨=4-
cos(φ+α)-4丨=4-![]() cos(φ+α)(tanα=
cos(φ+α)(tanα=![]() )當cos(φ+α)=1時,|x-y-4|取最小值,最小值為4-
)當cos(φ+α)=1時,|x-y-4|取最小值,最小值為4-![]() .
.


科目:高中數學 來源: 題型:
【題目】已知橢圓與拋物線y2=![]() x有一個相同的焦點,且該橢圓的離心率為
x有一個相同的焦點,且該橢圓的離心率為![]() .
.
(1)求橢圓的標準方程;
(2)過點P(0,1)的直線與該橢圓交于A,B兩點,O為坐標原點,若![]() ,求△AOB的面積.
,求△AOB的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地隨著經濟的發展,居民收入逐年增長,下表是該地一建設銀行連續五年的儲蓄存款(年底余額),如下表1:
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
儲蓄存款y(千億元) | 5 | 6 | 7 | 8 | 10 |
為了研究計算的方便,工作人員將上表的數據進行了處理, ![]() 得到下表2:
得到下表2:
時間代號t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
(Ⅰ)求z關于t的線性回歸方程;
(Ⅱ)通過(Ⅰ)中的方程,求出y關于x的回歸方程;
(Ⅲ)用所求回歸方程預測到2020年年底,該地儲蓄存款額可達多少?
(附:對于線性回歸方程![]() ,其中
,其中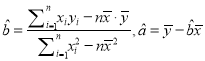 )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著“中華好詩詞”節目的播出,掀起了全民誦讀傳統詩詞經典的熱潮.某社團為調查大學生對于“中華詩詞”的喜好,從甲、乙兩所大學各隨機抽取了40名學生,記錄他們每天學習“中華詩詞”的時間,并整理得到如下頻率分布直方圖:

根據學生每天學習“中華詩詞”的時間,可以將學生對于“中華詩詞”的喜好程度分為三個等級 :
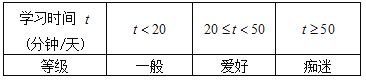
(Ⅰ)從甲大學中隨機選出一名學生,試估計其“愛好”中華詩詞的概率;
(Ⅱ)從兩組“癡迷”的同學中隨機選出2人,記![]() 為選出的兩人中甲大學的人數,求
為選出的兩人中甲大學的人數,求![]() 的分布列和數學期望
的分布列和數學期望![]() ;
;
(Ⅲ)試判斷選出的這兩組學生每天學習“中華詩詞”時間的平均值![]() 與
與![]() 的大小,及方差
的大小,及方差![]() 與
與![]() 的大小.(只需寫出結論)
的大小.(只需寫出結論)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 為坐標原點,動點
為坐標原點,動點![]() 在橢圓
在橢圓![]() 上,過
上,過![]() 作
作![]() 軸的垂線,垂足為
軸的垂線,垂足為![]() ,點
,點![]() 滿足
滿足![]() .(Ⅰ)求點
.(Ⅰ)求點![]() 的軌跡方程
的軌跡方程![]() ;
;
(Ⅱ)過![]() 的直線
的直線![]() 與點
與點![]() 的軌跡交于
的軌跡交于![]() 兩點,過
兩點,過![]() 作與
作與![]() 垂直的直線
垂直的直線![]() 與點
與點![]() 的軌跡交于
的軌跡交于![]() 兩點,求證:
兩點,求證: ![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左焦點
的左焦點![]() 與拋物線
與拋物線![]() 的焦點重合,橢圓
的焦點重合,橢圓![]() 的離心率為
的離心率為![]() ,過點
,過點![]() 作斜率不為0的直線
作斜率不為0的直線![]() ,交橢圓
,交橢圓![]() 于
于![]() 兩點,點
兩點,點![]() ,且
,且![]() 為定值.
為定值.
(1)求橢圓![]() 的方程;
的方程;
(2)求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com