
【題目】已知函數![]() .
.
(1)求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)求![]() 的單調區間;
的單調區間;
(3)若對于任意![]() ,都有
,都有![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() 的增區間是
的增區間是![]() ;
;
遞減區間是![]() ;(3)
;(3)![]() .
.
【解析】試題分析:(1)求出![]() 的值可得切點坐標,再求出
的值可得切點坐標,再求出![]() ,可得
,可得![]() 的值,即得切線斜率,利用點斜式可得曲線
的值,即得切線斜率,利用點斜式可得曲線![]() 在點
在點![]() 處的切線方程;(2)令
處的切線方程;(2)令![]() 求得
求得![]() 的范圍,可得函數
的范圍,可得函數![]() 增區間,
增區間, ![]() 求得
求得![]() 的范圍,可得函數
的范圍,可得函數![]() 的減區間;(3)對于任意
的減區間;(3)對于任意![]() ,都有
,都有![]() 等價于
等價于![]() ,令
,令![]() ,
, ![]() ,利用導數研究函數
,利用導數研究函數![]() 的單調性,求出函數
的單調性,求出函數![]() 的最大值,從而可得結果.
的最大值,從而可得結果.
試題解析:(1)因為函數![]() ,所以
,所以![]() ,
,
![]() .又因為
.又因為![]() ,
,
所以曲線![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() .
.
(2)函數![]() 定義域為
定義域為![]() , 由(1)可知,
, 由(1)可知, ![]() .
.
令![]() 解得
解得![]() .
.
![]() 與
與![]() 在區間
在區間![]() 上的情況如下:
上的情況如下:
|
|
|
|
|
|
|
|
| 減 | 極小值 | 增 |
所以, ![]() 的單調遞增區間是
的單調遞增區間是![]() ;
;
![]() 的單調遞減區間是
的單調遞減區間是![]() .
.
(3)當![]() 時,“
時,“![]() ”等價于“
”等價于“![]() ”.
”.
令![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
當![]() 時,
時, ![]() ,所以
,所以![]() 在區間
在區間![]() 單調遞減.
單調遞減.
當![]() 時,
時, ![]() ,所以
,所以![]() 在區間
在區間![]() 單調遞增.
單調遞增.
而![]() ,
,
![]() .
.
所以![]() 在區間
在區間![]() 上的最大值為
上的最大值為![]() .
.
所以當![]() 時,對于任意
時,對于任意![]() ,都有
,都有![]() .
.
【方法點晴】本題主要考查利用導數求曲線切線方程以及利用導數研究函數的單調性與不等式恒成立問題,屬于難題.不等式恒成立問題常見方法:① 分離參數![]() 恒成立(
恒成立(![]() 可)或
可)或![]() 恒成立(
恒成立(![]() 即可);② 數形結合(
即可);② 數形結合(![]() 圖象在
圖象在![]() 上方即可);③ 討論最值
上方即可);③ 討論最值![]() 或
或![]() 恒成立;④ 討論參數.本題(3)是利用方法 ① 求得實數
恒成立;④ 討論參數.本題(3)是利用方法 ① 求得實數![]() 的取值范圍.
的取值范圍.


 智能訓練練測考系列答案
智能訓練練測考系列答案科目:高中數學 來源: 題型:
【題目】某次有600人參加的數學測試,其成績的頻數分布表如圖所示,規定85分及其以上為優秀.
區間 | [75,80) | [80,85) | [85,90) | [90,95) | [95,100] |
人數 | 36 | 114 | 244 | 156 | 50 |
(Ⅰ)現用分層抽樣的方法從這600人中抽取20人進行成績分析,求其中成績為優秀的學生人數;
(Ⅱ)在(Ⅰ)中抽取的20名學生中,要隨機選取2名學生參加活動,記“其中成績為優秀的人數”為![]() ,求
,求![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
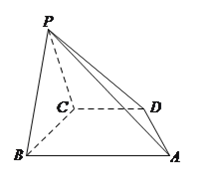
【題目】在四棱錐![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() .
.
(Ⅰ)求證: ![]() 平面
平面![]() .
.
(Ⅱ)求平面![]() 和平面
和平面![]() 所成二面角(小于
所成二面角(小于![]() )的大小.
)的大小.
(Ⅲ)在棱![]() 上是否存在點
上是否存在點![]() 使得
使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐PABCD中,AB∥CD ,且∠BAP=∠CDP =90°.
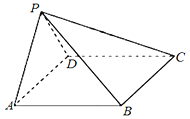
(1).證明:平面PAB⊥平面PAD;
(2).若PA=PD=AB=DC, ∠APD =90°,且四棱錐PABCD的體積為![]() ,求該四棱錐的側面積.
,求該四棱錐的側面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線![]() 的參數方程為
的參數方程為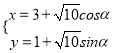 (
(![]() 為參數),以直角坐標系原點
為參數),以直角坐標系原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系.
軸正半軸為極軸,建立極坐標系.
(1)求曲線![]() 的極坐標方程,并說明其表示什么軌跡;
的極坐標方程,并說明其表示什么軌跡;
(2)若直線的極坐標方程為![]() ,求直線被曲線
,求直線被曲線![]() 截得的弦長.
截得的弦長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知直線![]() 的極坐標方程是
的極坐標方程是![]() ,以極點為原點,極軸為
,以極點為原點,極軸為![]() 軸的正半軸建立極坐標系,曲線
軸的正半軸建立極坐標系,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).
為參數).
(1)寫出直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設![]() 為曲線
為曲線![]() 上任意一點,求
上任意一點,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 在橢圓
在橢圓![]() 上,且橢圓的離心率為
上,且橢圓的離心率為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若![]() 為橢圓
為橢圓![]() 的右頂點,點
的右頂點,點![]() 是橢圓
是橢圓![]() 上不同的兩點(均異于
上不同的兩點(均異于![]() )且滿足直線
)且滿足直線![]() 與
與![]() 斜率之積為
斜率之積為![]() .試判斷直線
.試判斷直線![]() 是否過定點,若是,求出定點坐標,若不是,說明理由.
是否過定點,若是,求出定點坐標,若不是,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的準線與
的準線與![]() 軸交于點
軸交于點![]() ,過點
,過點![]() 做圓
做圓![]() 的兩條切線,切點為
的兩條切線,切點為![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)若直線![]() 是講過定點
是講過定點![]() 的一條直線,且與拋物線
的一條直線,且與拋物線![]() 交于
交于![]() 兩點,過定點
兩點,過定點![]() 作
作![]() 的垂線與拋物線交于
的垂線與拋物線交于![]() 兩點,求四邊形
兩點,求四邊形![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com