
【題目】在四棱錐![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
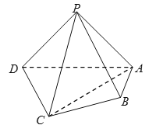
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)在棱![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
【答案】(1)見證明;(2)![]() (3)見解析
(3)見解析
【解析】
(1)由面面垂直的性質得![]() 面
面![]() ,即可證明
,即可證明![]() 面
面![]() (2)取
(2)取![]() 中點為
中點為![]() ,連結
,連結![]() ,
,![]() ,證明
,證明![]() , 以
, 以![]() 為原點,如圖建系易知
為原點,如圖建系易知![]() ,
,![]() ,
,![]() ,
,![]() ,求面
,求面![]() 及面
及面![]() 的法向量,利用二面角的向量公式求解即可(3)假設存在
的法向量,利用二面角的向量公式求解即可(3)假設存在![]() 點使得
點使得![]() ∥面
∥面![]() , 設
, 設![]() ,由
,由![]() ∥面
∥面![]() ,
,![]() 為
為![]() 的法向量,得
的法向量,得![]() ,
,
(1)∵面![]() 面
面![]() ,面
,面![]() 面
面![]() ,
,
∵![]() ,
,![]() 面
面![]() ,∴
,∴![]() 面
面![]() ,
,
∵![]() 面
面![]() , ∴
, ∴![]() ,
,
又![]() ,∴
,∴![]() 面
面![]() ,
,
(2)取![]() 中點為
中點為![]() ,連結
,連結![]() ,
,![]() ,
,
∵![]() , ∴
, ∴![]() ,
,
∵![]() , ∴
, ∴![]() ,
,
以![]() 為原點,如圖建系易知
為原點,如圖建系易知![]() ,
,![]() ,
,![]() ,
,![]() ,
,
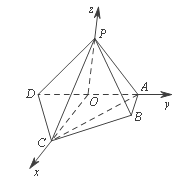
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
設![]() 為面
為面![]() 的法向量,令
的法向量,令![]() .
.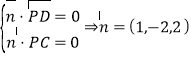 ,
,
設![]() 為面
為面![]() 的法向量,令
的法向量,令![]() .
.
 ,
,
則二面角![]() 余弦值為
余弦值為![]()
故二面角![]() 正弦值為
正弦值為![]()
(3)假設存在![]() 點使得
點使得![]() ∥面
∥面![]() , 設
, 設![]() ,
,![]() ,
,
由(2)知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
有![]() ∴
∴![]()
∵![]() ∥面
∥面![]() ,
,![]() 為
為![]() 的法向量,
的法向量,
∴![]() ,即
,即![]() ,得
,得![]()
綜上,存在![]() 點,即當
點,即當![]() 時,
時,![]() 點即為所求.
點即為所求.


科目:高中數學 來源: 題型:
【題目】程大位是明代著名數學家,他的《新編直指算法統宗》是中國歷史上一部影響巨大的著作,它問世后不久便風行宇內,成為明清之際研習數學者必讀的教材,而且傳到朝鮮、日本及東南亞地區,對推動漢字文化圈的數學發展起了重要的作用.卷八中第33問是:“今有三角果一垛,底闊每面七個,問該若干?”如圖是解決該問題的程序框圖,執行該程序框圖,求得該垛果子的總數![]() 為( )
為( )

A. 120 B. 84 C. 56 D. 28
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱錐P﹣ABC中,PA⊥平面ABC,△ABC是邊長為2的等邊三角形,且三棱錐P﹣ABC的外接球表面積為![]() ,則直線PC與平面PAB所成角的正切值為_____.
,則直線PC與平面PAB所成角的正切值為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在長方體ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,點E在棱AB上移動.
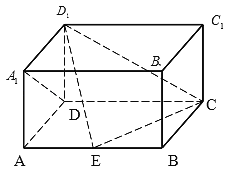
(1)證明:D1E⊥A1D;
(2)若EB![]() ,求二面角D1﹣EC﹣D的大小.
,求二面角D1﹣EC﹣D的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,圓形紙片的圓心為![]() ,半徑為
,半徑為![]() ,該紙片上的正方形
,該紙片上的正方形![]() 的中心為
的中心為![]() 為圓
為圓![]() 上的點,
上的點,![]() ,
,![]() ,
,![]() ,
,![]() 分別是以
分別是以![]() 為底邊的等腰三角形.沿虛線剪開后,分別以
為底邊的等腰三角形.沿虛線剪開后,分別以![]() 為折痕折起
為折痕折起![]() ,
,![]() ,
,![]() ,
,![]() 使得
使得![]() 重合,得到一個四棱錐.當該四棱錐的側面積是底面積的2倍時,該四棱錐的外接球的表面積為__________.
重合,得到一個四棱錐.當該四棱錐的側面積是底面積的2倍時,該四棱錐的外接球的表面積為__________.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() :
:![]() 的焦點為
的焦點為![]() ,準線為
,準線為![]() ,
,![]() 與
與![]() 軸的交點為
軸的交點為![]() ,點
,點![]() 在拋物線
在拋物線![]() 上,過點
上,過點![]() 作
作![]() 于點
于點![]() ,如圖1.已知
,如圖1.已知![]() ,且四邊形
,且四邊形![]() 的面積為
的面積為![]() .
.


(1)求拋物線![]() 的方程;
的方程;
(2)若正方形![]() 的三個頂點
的三個頂點![]() ,
,![]() ,
,![]() 都在拋物線
都在拋物線![]() 上(如圖2),求正方形
上(如圖2),求正方形![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 對于任意的
對于任意的![]()
![]() ,都有
,都有![]() ,當
,當![]() 時,
時,![]() ,且
,且![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)當![]() 時,求函數
時,求函數![]() 的最大值和最小值;
的最大值和最小值;
(3)設函數![]() ,判斷函數g(x) 最多有幾個零點,并求出此時實數m的取值范圍.
,判斷函數g(x) 最多有幾個零點,并求出此時實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 中,
中,![]() ,點
,點![]() 在直線
在直線![]() 上,其中
上,其中![]() .
.
(1)令![]() ,求證數列
,求證數列![]() 是等比數列;
是等比數列;
(2)求數列![]() 的通項;
的通項;
(3)設![]() 、
、![]() 分別為數列
分別為數列![]() 、
、![]() 的前
的前![]() 項和是否存在實數
項和是否存在實數![]() ,使得數列
,使得數列![]() 為等差數列?若存在,試求出
為等差數列?若存在,試求出![]() ,若不存在,則說明理由.
,若不存在,則說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com