
【題目】已知函數(shù)![]()
(1)若對任意![]() ,
,![]() 恒成立,求
恒成立,求![]() 的值;
的值;
(2)設(shè)![]() ,若
,若![]() 沒有零點(diǎn),求實(shí)數(shù)
沒有零點(diǎn),求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)對函數(shù)求導(dǎo)得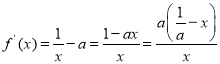 ,通過單調(diào)性可知當(dāng)
,通過單調(diào)性可知當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 取得極大值;若對任意
取得極大值;若對任意![]() ,
,![]() 在
在![]() 上恒成立,
上恒成立,
當(dāng)且僅當(dāng),![]() ,即
,即![]() 恒成立,得
恒成立,得![]() 即
即![]() ,構(gòu)造函數(shù)
,構(gòu)造函數(shù)![]() ,通過單調(diào)性求
,通過單調(diào)性求![]() 的值.
的值.
(2)![]() ,求導(dǎo)得
,求導(dǎo)得![]()
構(gòu)造函數(shù)![]() ,則
,則![]() 在區(qū)間
在區(qū)間![]() 內(nèi)存在唯一零點(diǎn)
內(nèi)存在唯一零點(diǎn)![]() ,通過單調(diào)性求得
,通過單調(diào)性求得![]() 的取值范圍.
的取值范圍.
解:(1)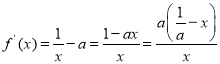 ,
,
當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() 在
在![]() 上是增函數(shù);
上是增函數(shù);
當(dāng)![]() 時(shí),
時(shí),![]() 在
在![]() 上是減函數(shù);
上是減函數(shù);
故當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 取得極大值
取得極大值![]() .
.
若對任意![]() ,
,![]() 在
在![]() 上恒成立,
上恒成立,
當(dāng)且僅當(dāng),![]() ,即
,即![]() 恒成立,
恒成立,
得![]() 即
即![]() .
.
設(shè)![]() ,則
,則![]() .
.
當(dāng)![]() 時(shí),
時(shí),![]() 是增函數(shù);
是增函數(shù);
當(dāng)![]() 時(shí),
時(shí),![]() 是減函數(shù),
是減函數(shù),
所以當(dāng)![]() 時(shí),
時(shí),![]() 取得極大值
取得極大值![]() ,得
,得![]() .
.
所以![]() ,可得
,可得![]() .
.
(2)![]() ,所以
,所以
![]() ,
,
設(shè)![]() ,則
,則![]() 在
在![]() 上是增函數(shù),
上是增函數(shù),
又![]() ,
,
所以![]() 在區(qū)間
在區(qū)間![]() 內(nèi)存在唯一零點(diǎn)
內(nèi)存在唯一零點(diǎn)![]() ,
,
即![]() .
.
當(dāng)![]() 時(shí),
時(shí),![]() ,即
,即![]() ;
;
當(dāng)![]() 時(shí),
時(shí),![]() ,即
,即![]() ,所以
,所以![]() 在
在![]() 上是減函數(shù),
上是減函數(shù),
在![]() 上是增函數(shù),所以
上是增函數(shù),所以![]() .
.
因?yàn)?/span>![]() 沒有零點(diǎn),所以
沒有零點(diǎn),所以![]() ,
,
即![]() ,所以
,所以![]() 的取值范圍是
的取值范圍是![]() .
.


 全優(yōu)點(diǎn)練單元計(jì)劃系列答案
全優(yōu)點(diǎn)練單元計(jì)劃系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某餐廳通過查閱了最近5次食品交易會(huì)參會(huì)人數(shù)![]() (萬人)與餐廳所用原材料數(shù)量
(萬人)與餐廳所用原材料數(shù)量![]() (袋),得到如下統(tǒng)計(jì)表:
(袋),得到如下統(tǒng)計(jì)表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
參會(huì)人數(shù) | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
(1)根據(jù)所給5組數(shù)據(jù),求出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() .
.
(2)已知購買原材料的費(fèi)用![]() (元)與數(shù)量
(元)與數(shù)量![]() (袋)的關(guān)系為
(袋)的關(guān)系為![]() ,
,
投入使用的每袋原材料相應(yīng)的銷售收入為700元,多余的原材料只能無償返還,據(jù)悉本次交易大會(huì)大約有15萬人參加,根據(jù)(1)中求出的線性回歸方程,預(yù)測餐廳應(yīng)購買多少袋原材料,才能獲得最大利潤,最大利潤是多少?(注:利潤![]() 銷售收入
銷售收入![]() 原材料費(fèi)用).
原材料費(fèi)用).
參考公式:  ,
, ![]() .
.
參考數(shù)據(jù): ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,一塊黃銅板上插著三根寶石針,在其中一根針上從下到上穿好由大到小的若干金片.若按照下面的法則移動(dòng)這些金片:每次只能移動(dòng)一片金片;每次移動(dòng)的金片必須套在某根針上;大片不能疊在小片上面.設(shè)移完n片金片總共需要的次數(shù)為an,可推得a1=1,an+1=2an+1.如圖是求移動(dòng)次數(shù)在1000次以上的最小片數(shù)的程序框圖模型,則輸出的結(jié)果是( )
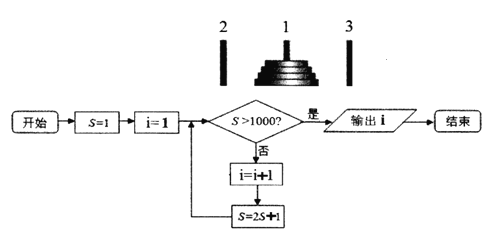
A. 8B. 9C. 10D. 11
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
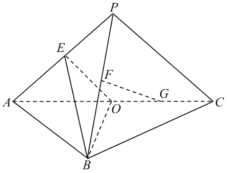
【題目】如圖,在三棱錐P—ABC中,平面PAC⊥平面ABC,AB=BC,PA⊥PC.點(diǎn)E,F,O分別為線段PA,PB,AC的中點(diǎn),點(diǎn)G是線段CO的中點(diǎn).
(1)求證:FG∥平面EBO;
(2)求證:PA⊥BE.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
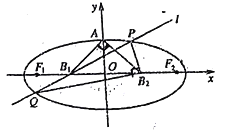
【題目】如圖,設(shè)橢圓的中心為原點(diǎn)![]() ,長軸在
,長軸在![]() 軸上,上頂點(diǎn)為
軸上,上頂點(diǎn)為![]() ,左右焦點(diǎn)分別為
,左右焦點(diǎn)分別為![]() ,線段
,線段![]() ,
,![]() 的中點(diǎn)分別為
的中點(diǎn)分別為![]() ,且
,且![]() 是面積為4的直角三角形,過
是面積為4的直角三角形,過![]() 作直線
作直線![]() 交橢圓于
交橢圓于![]() 兩點(diǎn),使
兩點(diǎn),使![]() ,則直線
,則直線![]() 的斜率為______.
的斜率為______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() 的方程為
的方程為![]() ,若拋物線
,若拋物線![]() 過點(diǎn)
過點(diǎn)![]() ,且以圓0的切線為準(zhǔn)線,
,且以圓0的切線為準(zhǔn)線,![]() 為拋物線的焦點(diǎn),點(diǎn)
為拋物線的焦點(diǎn),點(diǎn)![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)過點(diǎn)![]() 作直線
作直線![]() 交曲線
交曲線![]() 與
與![]() 兩點(diǎn),
兩點(diǎn),![]() 關(guān)于
關(guān)于![]() 軸對稱,請問:直線
軸對稱,請問:直線![]() 是否過
是否過![]() 軸上的定點(diǎn),如果不過請說明理由,如果過定點(diǎn),請求出定點(diǎn)
軸上的定點(diǎn),如果不過請說明理由,如果過定點(diǎn),請求出定點(diǎn)![]() 的坐標(biāo)
的坐標(biāo)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,邊長為a的空間四邊形ABCD中,∠BCD=90°,平面ABD⊥平面BCD,則異面直線AD與BC所成角的大小為( )
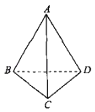
A. 30°B. 45°C. 60°D. 90°
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若函數(shù)![]() 在
在![]() 時(shí)取得極值,求實(shí)數(shù)
時(shí)取得極值,求實(shí)數(shù)![]() 的值;
的值;
(2)若![]() 對任意
對任意![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】國內(nèi)某知名企業(yè)為適應(yīng)發(fā)展的需要,計(jì)劃加大對研發(fā)的投入,據(jù)了解,該企業(yè)原有100名技術(shù)人員,年人均投入![]() 萬元,現(xiàn)把原有技術(shù)人員分成兩部分:技術(shù)人員和研發(fā)人員,其中技術(shù)人員
萬元,現(xiàn)把原有技術(shù)人員分成兩部分:技術(shù)人員和研發(fā)人員,其中技術(shù)人員![]() 名(
名(![]() 且
且![]() ),調(diào)整后研發(fā)人員的年人均投入增加
),調(diào)整后研發(fā)人員的年人均投入增加![]() %,技術(shù)人員的年人均投入調(diào)整為
%,技術(shù)人員的年人均投入調(diào)整為![]() 萬元.
萬元.
(1)要使這![]() 名研發(fā)人員的年總投入恰好與調(diào)整前100名技術(shù)人員的年總投入相同,求調(diào)整后的技術(shù)人員的人數(shù);
名研發(fā)人員的年總投入恰好與調(diào)整前100名技術(shù)人員的年總投入相同,求調(diào)整后的技術(shù)人員的人數(shù);
(2)是否存在這樣的實(shí)數(shù)![]() ,使得調(diào)整后,在技術(shù)人員的年人均投入不減少的情況下,研發(fā)人員的年總投入始終不低于技術(shù)人員的年總投入?若存在,求出
,使得調(diào)整后,在技術(shù)人員的年人均投入不減少的情況下,研發(fā)人員的年總投入始終不低于技術(shù)人員的年總投入?若存在,求出![]() 的范圍,若不存在,說明理由.
的范圍,若不存在,說明理由.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com