【題目】已知函數
.
（1）若函數
在
時取得極值，求實數
的值；
（2）若
對任意
恒成立，求實數的取值范圍.
王后雄學案教材完全解讀系列答案
海淀課時新作業金榜卷系列答案
期末金牌卷系列答案
輕松課堂標準練系列答案科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，直線
的參數方程為
（
為參數），直線
與直線平行，且過坐標原點，圓
的參數方程為
（
為參數）．以坐標原點為極點，
軸的正半軸為極軸建立極坐標系．
（1）求直線和圓的極坐標方程；
（2）設直線和圓相交于點
、
兩點，求
的周長．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，橢圓
：
的離心率為
，左、右頂點分別為
、
，線段
的長為4.點
在橢圓上且位于第一象限，過點，分別作
，
，直線
，
交于點
.
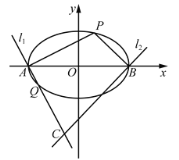
（1）若點的橫坐標為-1，求點的坐標；
（2）直線與橢圓的另一交點為
，且
，求
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】記無窮數列
的前n項中最大值為
，最小值為
，令
，數列的前n項和為
，數列
的前n項和為
．
（1）若數列是首項為2，公比為2的等比數列，求；
（2）若數列是等差數列，試問數列是否也一定是等差數列？若是，請證明；若不是，請舉例說明；
（3）若
，求．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系中，設點
，定義
，其中
為坐標原點，對于下列結論：
符合
的點
的軌跡圍成的圖形面積為8；
設點是直線：
上任意一點，則
；
設點是直線：
上任意一點，則使得“
最小的點有無數個”的充要條件是
；
設點是橢圓
上任意一點，則
．
其中正確的結論序號為
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系中，設點
，定義
，其中
為坐標原點，對于下列結論：
符合
的點
的軌跡圍成的圖形面積為8；
設點是直線：
上任意一點，則
；
設點是直線：
上任意一點，則使得“
最小的點有無數個”的必要條件是
；
設點是圓
上任意一點，則
．
其中正確的結論序號為
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】甲、乙兩人同時參加一個外貿公司的招聘,招聘分筆試與面試兩部分,先筆試后面試.甲筆試與面試通過的概率分別為0.8,0.5,乙筆試與面試通過的概率分別為0.8,0.4,且筆試通過了才能進入面試,面試通過則直接招聘錄用,兩人筆試與面試相互獨立互不影響.
(1)求這兩人至少有一人通過筆試的概率;
(2)求這兩人筆試都通過卻都未被錄用的概率;
(3)記這兩人中最終被錄用的人數為X,求X的分布列和數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某運動會將在深圳舉行，組委會招募了12名男志愿者和18名女志愿者，將這30名志愿者的身高編成如圖所示的莖葉圖（單位：
），身高在
以上（包括）定義為“高個子”，身高在以下（不包括）定義為“非高個子”．
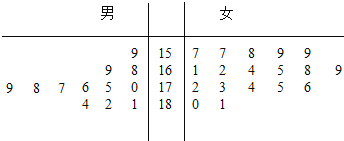
（1）如果用分層抽樣的方法從“高個子”和“非高個子”中抽取5人，再從這5人中選2人，求至少有一人是“高個子”的概率；
（2）若從身高
以上（包括）的志愿者中選出男、女各一人，設這2人身高相差
（
），求
的分布列和數學期望（均值）．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
