
【題目】如圖所示,邊長為a的空間四邊形ABCD中,∠BCD=90°,平面ABD⊥平面BCD,則異面直線AD與BC所成角的大小為( )
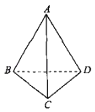
A. 30°B. 45°C. 60°D. 90°
【答案】C
【解析】
由題意得![]() ,
,![]() ,從而
,從而![]() ,
,![]() ,取
,取![]() 中點
中點![]() ,連結
,連結![]() ,
,![]() ,從而
,從而![]() 平面
平面![]() ,延長
,延長![]() 至點
至點![]() ,使
,使![]() ,連結
,連結![]() ,
,![]() ,
,![]() ,則四邊形
,則四邊形![]() 為正方形,即有
為正方形,即有![]() ,從而
,從而![]() (或其補角)即為異面直線
(或其補角)即為異面直線![]() 與
與![]() 所成角,由此能求出異面直線
所成角,由此能求出異面直線![]() 與
與![]() 所成角的大小.
所成角的大小.
由題意得BC=CD=a,∠BCD=90°,
∴BD=![]() ,∴∠BAD=90°,
,∴∠BAD=90°,
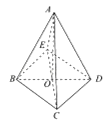
取BD中點O,連結AO,CO,
∵AB=BC=CD=DA=a,
∴AO⊥BD,CO⊥BD,且AO=BO=OD=OC=![]() ,
,
又∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AO⊥BD,
∴AO⊥平面BCD,
延長CO至點E,使CO=OE,連結ED,EA,EB,
則四邊形BCDE為正方形,即有BC∥DE,
∴∠ADE(或其補角)即為異面直線AD與BC所成角,
由題意得AE=a,ED=a,
∴△AED為正三角形,∴∠ADE=60°,
∴異面直線AD與BC所成角的大小為60°.
故選:C.


科目:高中數學 來源: 題型:
【題目】某中學高一期中考試結束后,從高一年級1000名學生中任意抽取50名學生,將這50名學生的某一科的考試成績(滿分150分)作為樣本進行統計,并作出樣本成績的頻率分布直方圖(如圖).
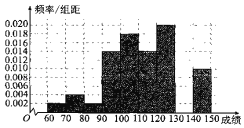
(1)由于工作疏忽,將成績[130,140)的數據丟失,求此區間的人數及頻率分布直方圖的中位數;(結果保留兩位小數)
(2)若規定考試分數不小于120分為優秀,現從樣本的優秀學生中任意選出3名學生,參加學習經驗交流會.設X表示參加學習經驗交流會的學生分數不小于130分的學生人數,求X的分布列及期望;
(3)視樣本頻率為概率.由于特殊原因,有一個學生不能到學校參加考試,根據以往考試成績,一般這名學生的成績應在平均分左右.試根據以上數據,說明他若參加考試,可能得多少分?(每組數據以區問的中點值為代表)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
以平面直角坐標系xOy的原點為極點,x軸的正半軸為極軸,取相同的長度單位建立極坐標系,直線l的坐標方程為![]() ,曲線C的參數方程為
,曲線C的參數方程為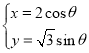 (θ為參數).
(θ為參數).
(1)求直線l的直角坐標方程和曲線C的普通方程;
(2)以曲線C上的動點M為圓心、r為半徑的圓恰與直線l相切,求r的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠的機器上存在一種易損元件,這種元件發生損壞時,需要及時維修. 現有甲、乙兩名工人同時從事這項工作,下表記錄了某月1日到10日甲、乙兩名工人分別維修這種元件的件數.
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 | 8日 | 9日 | 10日 |
甲維修的元件數 | 3 | 5 | 4 | 6 | 4 | 6 | 3 | 7 | 8 | 4 |
乙維修的元件數 | 4 | 7 | 4 | 5 | 5 | 4 | 5 | 5 | 4 | 7 |
(1)從這![]() 天中,隨機選取一天,求甲維修的元件數不少于5件的概率;
天中,隨機選取一天,求甲維修的元件數不少于5件的概率;
(2)試比較這10天中甲維修的元件數的方差![]() 與乙維修的元件數的方差
與乙維修的元件數的方差![]() 的大小.(只需寫出結論);
的大小.(只需寫出結論);
(3)由于甲、乙的任務量大,擬增加工人,為使增加工人后平均每人每天維修的元件不超過3件,請利用上表數據估計最少需要增加幾名工人.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com