
【題目】某中學高一期中考試結束后,從高一年級1000名學生中任意抽取50名學生,將這50名學生的某一科的考試成績(滿分150分)作為樣本進行統計,并作出樣本成績的頻率分布直方圖(如圖).
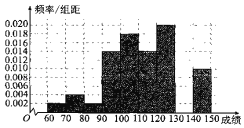
(1)由于工作疏忽,將成績[130,140)的數據丟失,求此區間的人數及頻率分布直方圖的中位數;(結果保留兩位小數)
(2)若規定考試分數不小于120分為優秀,現從樣本的優秀學生中任意選出3名學生,參加學習經驗交流會.設X表示參加學習經驗交流會的學生分數不小于130分的學生人數,求X的分布列及期望;
(3)視樣本頻率為概率.由于特殊原因,有一個學生不能到學校參加考試,根據以往考試成績,一般這名學生的成績應在平均分左右.試根據以上數據,說明他若參加考試,可能得多少分?(每組數據以區問的中點值為代表)
【答案】(1)8, 117.14;(2)見解析;(3)115.4
【解析】
(1)先求出這50名學生成績在各區間的頻率及人數,由此能求出![]() ,
,![]() 的頻率為0.16,人數為8,從而能求出中位數.(2)考試分數不小于120分的優秀學生有23人,
的頻率為0.16,人數為8,從而能求出中位數.(2)考試分數不小于120分的優秀學生有23人,![]() 表示參加教學交流會的不小于130分的學生人數的取值為0,1,2,3,分別求出相應的概率,由此能求出
表示參加教學交流會的不小于130分的學生人數的取值為0,1,2,3,分別求出相應的概率,由此能求出![]() 的分布列和
的分布列和![]() .(3)利用頻率分布直方圖能求出平均分.
.(3)利用頻率分布直方圖能求出平均分.
(1)這50名學生成績在各區間的頻率及人數如下:[60,70)的頻率為0.02,人數為1,
[70,80)的頻率為0.04,人數為2,[80,90)的頻率為0.02,人數為1,
[90,100)的頻率為0.14,人數為7,[100,110)的頻率為0.18,人數為9,
[110,120)的頻率為0.14,人數為7,[120,130)的頻率為0.2,人數為10,
[140,150)的頻率為0.1,人數為5,∴[130,140)的頻率為0.16,人數為8,
∵中位數把頻率分布直方圖分成左右面積相等,設中位數為m,[60,110)的頻率和為:
0.02+0.04+0.02+0.14+0.18=0.4,[110,120)的頻率為0.14,
∴(m﹣110)×0.14=0.5﹣0.4=0.1,解得m=![]() ≈117.14.
≈117.14.
所以頻率分布直方圖的中位數為117.14.
(2)考試分數不小于120分的優秀學生有23人,X表示參加教學交流會的不小于130分的學生人數的取值為0,1,2,3,
P(X=0)=![]() ,
,
P(X=1)=![]() ,
,
P(X=2)=![]() ,
,
P(X=3)![]() ,
,
∴X的分布列為:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
E(X)![]() ;
;
(3)平均分W=65×0.02+75×0.04+85×0.02+95×0.14+105×0.18+115×0.14+125×0.2+135×0.16+145×0.1=115.4,
∴該學生可能得分為115.4分.


科目:高中數學 來源: 題型:
【題目】從某商場隨機抽取了2000件商品,按商品價格(元)進行統計,所得頻率分布直方圖如圖所示.記價格在![]() ,
,![]() ,
,![]() 對應的小矩形的面積分別為
對應的小矩形的面積分別為![]() ,且
,且![]() .
.
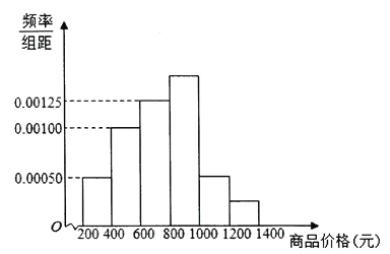
(1)按分層抽樣從價格在![]() ,
,![]() 的商品中共抽取6件,再從這6件中隨機抽取2件作價格對比,求抽到的兩件商品價格差超過800元的概率;
的商品中共抽取6件,再從這6件中隨機抽取2件作價格對比,求抽到的兩件商品價格差超過800元的概率;
(2)在清明節期間,該商場制定了兩種不同的促銷方案:
方案一:全場商品打八折;
方案二:全場商品優惠如下表,如果你是消費者,你會選擇哪種方案?為什么?(同一組中的數據用該組區間中點值作代表)
商品價格 |
|
|
|
|
|
|
優惠(元) | 30 | 50 | 140 | 160 | 280 | 320 |
查看答案和解析>>
科目:高中數學 來源: 題型:
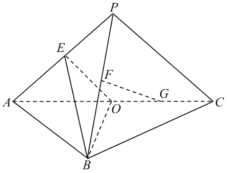
【題目】如圖,在三棱錐P—ABC中,平面PAC⊥平面ABC,AB=BC,PA⊥PC.點E,F,O分別為線段PA,PB,AC的中點,點G是線段CO的中點.
(1)求證:FG∥平面EBO;
(2)求證:PA⊥BE.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 的方程為
的方程為![]() ,若拋物線
,若拋物線![]() 過點
過點![]() ,且以圓0的切線為準線,
,且以圓0的切線為準線,![]() 為拋物線的焦點,點
為拋物線的焦點,點![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)過點![]() 作直線
作直線![]() 交曲線
交曲線![]() 與
與![]() 兩點,
兩點,![]() 關于
關于![]() 軸對稱,請問:直線
軸對稱,請問:直線![]() 是否過
是否過![]() 軸上的定點,如果不過請說明理由,如果過定點,請求出定點
軸上的定點,如果不過請說明理由,如果過定點,請求出定點![]() 的坐標
的坐標
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,邊長為a的空間四邊形ABCD中,∠BCD=90°,平面ABD⊥平面BCD,則異面直線AD與BC所成角的大小為( )
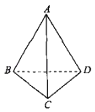
A. 30°B. 45°C. 60°D. 90°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C的中心在原點,焦點在x軸上,短軸長為![]() ,離心率為
,離心率為![]() .
.
![]() Ⅰ
Ⅰ![]() 求橢圓C的方程;
求橢圓C的方程;
![]() Ⅱ
Ⅱ![]() 若過點
若過點![]() 的直線與橢圓C交于A,B兩點,且P點平分線段AB,求直線AB的方程;
的直線與橢圓C交于A,B兩點,且P點平分線段AB,求直線AB的方程;
![]() Ⅲ
Ⅲ![]() 一條動直線l與橢圓C交于不同兩點M,N,O為坐標原點,
一條動直線l與橢圓C交于不同兩點M,N,O為坐標原點,![]() 的面積為
的面積為![]() 求證:
求證:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在全國第五個“扶貧日”到來之前,某省開展“精準扶貧,攜手同行”的主題活動,某貧困縣調查基層干部走訪貧困戶數量.甲鎮有基層干部60人,乙鎮有基層干部60人,丙鎮有基層干部80人,每人都走訪了若干貧困戶,按照分層抽樣,從甲、乙、丙三鎮共選20名基層干部,統計他們走訪貧困戶的數量,并將走訪數量分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 5組,繪制成如圖所示的頻率分布直方圖.
5組,繪制成如圖所示的頻率分布直方圖.
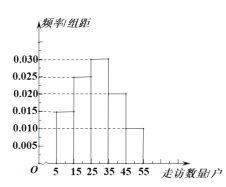
(1)求這20人中有多少人來自丙鎮,并估計甲、乙、丙三鎮的基層干部走訪貧困戶戶數的中位數(精確到整數位);
(2)如果把走訪貧困戶達到或超過35戶視為工作出色,求選出的20名基層干部中工作出色的人數,并從中選2人做交流發言,求這2人中至少有一人走訪的貧困戶在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知平面內兩個定點![]() 和點
和點![]() ,
,![]() 是動點,且直線
是動點,且直線![]() ,
,![]() 的斜率乘積為常數
的斜率乘積為常數![]() ,設點
,設點![]() 的軌跡為
的軌跡為![]() .
.
① 存在常數![]() ,使
,使![]() 上所有點到兩點
上所有點到兩點![]() 距離之和為定值;
距離之和為定值;
② 存在常數![]() ,使
,使![]() 上所有點到兩點
上所有點到兩點![]() 距離之和為定值;
距離之和為定值;
③ 不存在常數![]() ,使
,使![]() 上所有點到兩點
上所有點到兩點![]() 距離差的絕對值為定值;
距離差的絕對值為定值;
④ 不存在常數![]() ,使
,使![]() 上所有點到兩點
上所有點到兩點![]() 距離差的絕對值為定值.
距離差的絕對值為定值.
其中正確的命題是_______________.(填出所有正確命題的序號)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com