
 的前
的前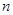 項和是
項和是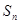 ,滿足
,滿足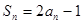 .
. 的通項
的通項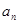 及前
及前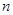 項和
項和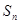 ;
;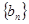 滿足
滿足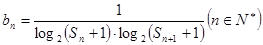 ,求數(shù)列
,求數(shù)列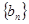 的前
的前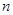 項和
項和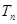 ;
;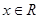 ,恒有
,恒有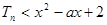 成立,求實數(shù)
成立,求實數(shù)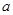 的取值范圍
的取值范圍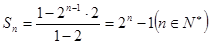 . (2)
. (2)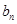
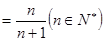
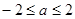
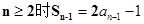 ,再與
,再與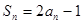 作差可得
作差可得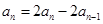 ,進(jìn)而確定
,進(jìn)而確定 是等比數(shù)列.問題得解.
是等比數(shù)列.問題得解.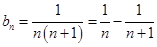 采用裂項求和方法求和.
采用裂項求和方法求和.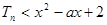 恒成立 , 即
恒成立 , 即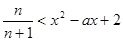 恒成立
恒成立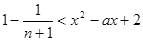 恒成立 ,必須且只須滿足
恒成立 ,必須且只須滿足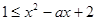 恒成立,然后轉(zhuǎn)化為關(guān)于
恒成立,然后轉(zhuǎn)化為關(guān)于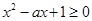 對于一切實數(shù)x恒成立即可.
對于一切實數(shù)x恒成立即可.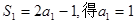 ,…………1分
,…………1分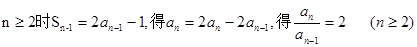 ---------2分
---------2分 是等比數(shù)列
是等比數(shù)列 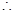 數(shù)列
數(shù)列 的公比q="2"
的公比q="2"  的通項公式為
的通項公式為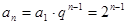
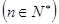 …………3分
…………3分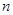 項和公式為
項和公式為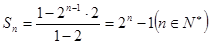 . ………………………4分
. ………………………4分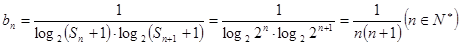
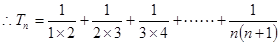 ……………………………6分
……………………………6分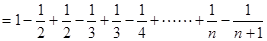 ………………………7分
………………………7分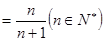 …………………………………………8分
…………………………………………8分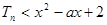 恒成立 即
恒成立 即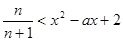 恒成立
恒成立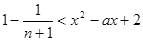 恒成立 ……………………………………9分
恒成立 ……………………………………9分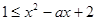 恒成立 ………………………………10分
恒成立 ………………………………10分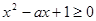 在R上恒成立
在R上恒成立 
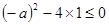 ,………………11分
,………………11分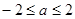 .
. 

科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
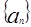 滿足
滿足 ,則稱數(shù)列
,則稱數(shù)列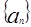 為“等方比數(shù)列”甲:數(shù)列
為“等方比數(shù)列”甲:數(shù)列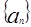 為“等比數(shù)列”;乙:數(shù)列
為“等比數(shù)列”;乙:數(shù)列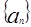 為“等方比數(shù)列”;則
為“等方比數(shù)列”;則| A.甲是乙的充分不必要條件, |
| B.甲是乙的必要不充分條件, |
| C.甲是乙的充要條件, |
| D.甲既不是乙的充分條件也不是乙的必要條件, |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
 的首項
的首項 ,前
,前 項和
項和 .(Ⅰ)求數(shù)列
.(Ⅰ)求數(shù)列 的通項公式;(Ⅱ)設(shè)
的通項公式;(Ⅱ)設(shè) ,
, ,
, 為數(shù)列
為數(shù)列 的前
的前 項和,求證:
項和,求證: .
.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
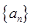 中,
中,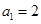 ,
,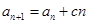 (
(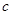 是常數(shù),
是常數(shù),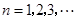 ),且
),且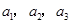 成公比不為
成公比不為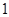 的等比數(shù)列。
的等比數(shù)列。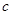 的值;
的值;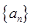 的通項公式。
的通項公式。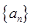 中的第1、3、9、27、……項構(gòu)成一個新的數(shù)列{b
中的第1、3、9、27、……項構(gòu)成一個新的數(shù)列{b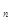 },求
},求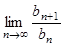 的值。
的值。查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
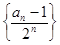 為等差數(shù)列;
為等差數(shù)列;查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
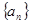 ,若
,若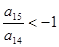 ,且它的前
,且它的前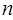 項和
項和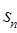 有最大值,那么當(dāng)
有最大值,那么當(dāng)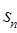 取得最小正值時,
取得最小正值時,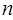 =( )
=( )| A.14 | B.15 | C.27 | D.28 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com