
【題目】如圖所示,![]() 和
和![]() 所在平面互相垂直,且
所在平面互相垂直,且![]() ,
,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點.
的中點.

(1)求證:![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
【答案】(1)見解析(2) ![]()
【解析】
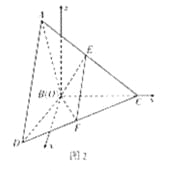
試題分析:(1)(方法一)過E作EO⊥BC,垂足為O,連OF,由△ABC≌△DBC可證出△EOC≌△FOC,所以∠EOC=∠FOC=![]() ,即FO⊥BC,又EO⊥BC,因此BC⊥面EFO,即可證明EF⊥BC.(方法二)由題意,以B為坐標原點,在平面DBC內過B左垂直BC的直線為x軸,BC所在直線為y軸,在平面ABC內過B作垂直BC的直線為z軸,建立如圖所示的空間直角坐標系.
,即FO⊥BC,又EO⊥BC,因此BC⊥面EFO,即可證明EF⊥BC.(方法二)由題意,以B為坐標原點,在平面DBC內過B左垂直BC的直線為x軸,BC所在直線為y軸,在平面ABC內過B作垂直BC的直線為z軸,建立如圖所示的空間直角坐標系.
易得![]() ,所以
,所以![]() ,因此
,因此![]() ,從而得
,從而得![]() ;(2) (方法一)在圖1中,過O作OG⊥BF,垂足為G,連EG,由平面ABC⊥平面BDC,從而EO⊥平面BDC,從而EO⊥面BDC,又OG⊥BF,由三垂線定理知EG垂直BF,因此∠EGO為二面角E-BF-C的平面角;在△EOC中,EO=
;(2) (方法一)在圖1中,過O作OG⊥BF,垂足為G,連EG,由平面ABC⊥平面BDC,從而EO⊥平面BDC,從而EO⊥面BDC,又OG⊥BF,由三垂線定理知EG垂直BF,因此∠EGO為二面角E-BF-C的平面角;在△EOC中,EO=![]() EC=
EC=![]() BC·cos30°=
BC·cos30°=![]() ,由△BGO∽△BFC知,
,由△BGO∽△BFC知,![]() ,因此tan∠EGO=
,因此tan∠EGO=![]() ,從而sin∠EGO=
,從而sin∠EGO=![]() ,即可求出二面角E-BF-C的正弦值.
,即可求出二面角E-BF-C的正弦值.
(方法二)在圖2中,平面BFC的一個法向量為![]() ,設平面BEF的法向量
,設平面BEF的法向量![]() ,又,由
,又,由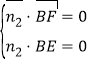 得其中一個
得其中一個![]() ,設二面角E-BF-C的大小為
,設二面角E-BF-C的大小為![]() ,且由題意知
,且由題意知![]() 為銳角,則
為銳角,則 ,因此sin∠EGO=
,因此sin∠EGO=![]() ,即可求出二面角E-BF-C的正弦值.
,即可求出二面角E-BF-C的正弦值.
(1)證明:
(方法一)過E作EO⊥BC,垂足為O,連OF,
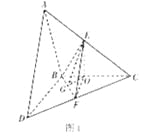
由△ABC≌△DBC可證出△EOC≌△FOC,所以∠EOC=∠FOC=![]() ,即FO⊥BC,
,即FO⊥BC,
又EO⊥BC,因此BC⊥面EFO,
又EF![]() 面EFO,所以EF⊥BC.
面EFO,所以EF⊥BC.
(方法二)由題意,以B為坐標原點,在平面DBC內過B左垂直BC的直線為x軸,BC所在直線為y軸,在平面ABC內過B作垂直BC的直線為z軸,建立如圖所示的空間直角坐標系.
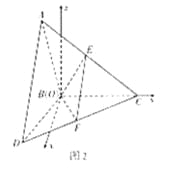
易得B(0,0,0),A(0,-1,![]() ),D(
),D(![]() ,-1,0),C(0,2,0),因而
,-1,0),C(0,2,0),因而![]() ,所以
,所以![]() ,因此
,因此![]() ,從而
,從而![]() ,所以
,所以![]() .
.
(2)(方法一)在圖1中,過O作OG⊥BF,垂足為G,連EG,由平面ABC⊥平面BDC,從而EO⊥平面BDC,從而EO⊥面BDC,又OG⊥BF,由三垂線定理知EG垂直BF.
因此∠EGO為二面角E-BF-C的平面角;
在△EOC中,EO=![]() EC=
EC=![]() BC·cos30°=
BC·cos30°=![]() ,由△BGO∽△BFC知,
,由△BGO∽△BFC知,![]() ,因此tan∠EGO=
,因此tan∠EGO=![]() ,從而sin∠EGO=
,從而sin∠EGO=![]() ,即二面角E-BF-C的正弦值為
,即二面角E-BF-C的正弦值為![]() .
.
(方法二)在圖2中,平面BFC的一個法向量為![]() ,設平面BEF的法向量
,設平面BEF的法向量![]() ,又
,又![]() ,由
,由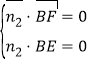 得其中一個
得其中一個![]() ,設二面角E-BF-C的大小為
,設二面角E-BF-C的大小為![]() ,且由題意知
,且由題意知![]() 為銳角,則
為銳角,則 ,因此sin∠EGO=
,因此sin∠EGO=![]() ,即二面角E-BF-C的正弦值為
,即二面角E-BF-C的正弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】甲、乙、丙三人玩摸卡片游戲,現有標號為1到12的卡片共12張,每人摸4張.
甲說:我摸到卡片的標號是10和12;
乙說:我摸到卡片的標號是6和11;
丙說:我們三人各自摸到卡片的標號之和相等.
據此可判斷丙摸到的編號中必有的兩個是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某小組共有10人,利用假期參加義工活動,已知參加義工活動1次的有2人、2次的有4人、3次的有4人.現從這10人中隨機選出2人作為該組代表參加座談會.
(I)設![]() 為事件“選出的2人參加義工活動次數之和為4”,求事件
為事件“選出的2人參加義工活動次數之和為4”,求事件![]() 發生的概率;
發生的概率;
(II)設![]() 為選出的2人參加義工活動次數之差的絕對值,求隨機變量
為選出的2人參加義工活動次數之差的絕對值,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】水葫蘆原產于巴西,![]() 年作為觀賞植物引入中國. 現在南方一些水域水葫蘆已泛濫成災嚴重影響航道安全和水生動物生長. 某科研團隊在某水域放入一定量水葫蘆進行研究,發現其蔓延速度越來越快,經過
年作為觀賞植物引入中國. 現在南方一些水域水葫蘆已泛濫成災嚴重影響航道安全和水生動物生長. 某科研團隊在某水域放入一定量水葫蘆進行研究,發現其蔓延速度越來越快,經過![]() 個月其覆蓋面積為
個月其覆蓋面積為![]() ,經過
,經過![]() 個月其覆蓋面積為
個月其覆蓋面積為![]() . 現水葫蘆覆蓋面積
. 現水葫蘆覆蓋面積![]() (單位
(單位![]() )與經過時間
)與經過時間![]() 個月的關系有兩個函數模型
個月的關系有兩個函數模型![]() 與
與![]() 可供選擇.
可供選擇.
(參考數據:![]() )
)
(Ⅰ)試判斷哪個函數模型更合適,并求出該模型的解析式;
(Ⅱ)求原先投放的水葫蘆的面積并求約經過幾個月該水域中水葫蘆面積是當初投放的![]() 倍.
倍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知拋物線![]() 經過
經過![]() ,
,![]() 兩點,與
兩點,與![]() 軸的另一個交點為
軸的另一個交點為![]() ,頂點為
,頂點為![]() ,連結
,連結![]() .
.

(1)求該拋物線的表達式;
(2)點![]() 為該拋物線上的一動點(與點
為該拋物線上的一動點(與點![]() 、
、![]() 不重合),設點
不重合),設點![]() 的橫坐標為
的橫坐標為![]() .當點
.當點![]() 在直線
在直線![]() 的下方運動時,求
的下方運動時,求![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解少年兒童的肥胖是否與常喝碳酸飲料有關,現對![]() 名六年級學生進行了問卷調查,得到如下列聯表(平均每天喝
名六年級學生進行了問卷調查,得到如下列聯表(平均每天喝![]() 以上為常喝,體重超過
以上為常喝,體重超過![]() 為肥胖):
為肥胖):
常喝 | 不常喝 | 合計 | |
肥胖 |
|
|
|
不胖 |
|
|
|
合計 |
|
|
|
(1)已知在全部![]() 人中隨機抽取
人中隨機抽取![]() 人,求抽到肥胖的學生的概率?
人,求抽到肥胖的學生的概率?
(2)是否有![]() 的把握認為肥胖與常喝碳酸飲料有關?說明你的理由;
的把握認為肥胖與常喝碳酸飲料有關?說明你的理由;
(3)現從常喝碳酸飲料且肥胖的學生中(其中![]() 名女生),抽取
名女生),抽取![]() 人參加電視節目,則正好抽到一男一女的概率是多少?
人參加電視節目,則正好抽到一男一女的概率是多少?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(參考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列五個結論,其中正確的結論是( )
A.函數![]() 的最大值為
的最大值為![]()
B.已知函數![]() (
(![]() 且
且![]() )在
)在![]() 上是減函數則a的取值范圍是
上是減函數則a的取值范圍是![]()
C.在同一直角坐標系中,函數![]() 與
與![]() 的圖象關于y軸對稱
的圖象關于y軸對稱
D.在同一直角坐標系中,函數![]() 與
與![]() 的圖象關于直線
的圖象關于直線![]() 對稱
對稱
E.已知定義在R上的奇函數![]() 在
在![]() 內有1010個零點,則函數
內有1010個零點,則函數![]() 的零點個數為2021
的零點個數為2021
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工科院校對A、B兩個專業的男、女生人數進行調查統計,得到以下表格:
專業A | 專業B | 合計 | |
女生 | 12 | ||
男生 | 46 | 84 | |
合計 | 50 | 100 |
如果認為工科院校中“性別”與“專業”有關,那么犯錯誤的概率不會超過( )
注:![]()
P(x2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
A. 0.005B. 0.01C. 0.025D. 0.05
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com