
 ,動圓
,動圓 過點
過點 且與圓
且與圓 相切,記動圓圓
相切,記動圓圓 的軌跡為
的軌跡為 .
. 的方程;
的方程; 為曲線
為曲線 上任意一點,證明直線
上任意一點,證明直線 與曲線
與曲線 恒有且只有一個公共點.
恒有且只有一個公共點. 寫出一個類似的結(jié)論(皆不必證明).
寫出一個類似的結(jié)論(皆不必證明). 圓心為
圓心為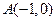 ,半徑為
,半徑為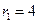 ,設(shè)動圓
,設(shè)動圓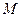 的圓心為
的圓心為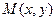
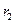 ,
,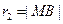 ,由
,由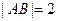 ,可知點
,可知點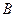 在圓
在圓 內(nèi),所以點
內(nèi),所以點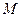 的軌跡是以
的軌跡是以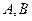 為焦點
為焦點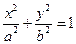
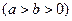 ,由
,由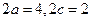 ,得
,得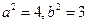 ,
, 的方程為
的方程為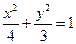 ………………………………4分
………………………………4分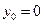 時,由
時,由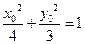 可得
可得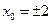
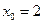 ,
,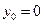 時,直線
時,直線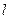 的方程為
的方程為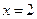 ,直線
,直線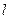 與曲線
與曲線 有且只有一個交點
有且只有一個交點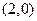
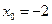 ,
,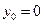 時,直線
時,直線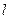 的方程為
的方程為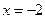 ,直線
,直線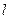 與曲線
與曲線 有且只有一個交點
有且只有一個交點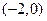
 時得
時得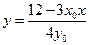 ,代入
,代入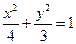 ,消去
,消去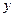 整理得:
整理得: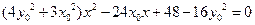 --------------------------------① …………6分
--------------------------------① …………6分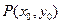 為曲線
為曲線 上一點,故
上一點,故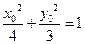 .即
.即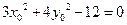
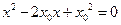
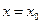 .將
.將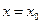 代入
代入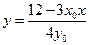 得
得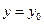 ,說明直線與曲線有且只有一個交點
,說明直線與曲線有且只有一個交點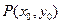 .
.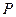 在何位置,直線
在何位置,直線 :
: 與曲線
與曲線 恒有且只有一個交點,交點即
恒有且只有一個交點,交點即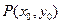 …………………………………………8分
…………………………………………8分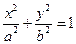
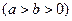 ,過其上任意一點
,過其上任意一點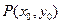 的切線方程為
的切線方程為 ;
; 中的類似的結(jié)論是:過雙曲線
中的類似的結(jié)論是:過雙曲線 上任意一點
上任意一點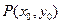 的切線方程為:
的切線方程為: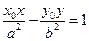 .…………………………………12分
.…………………………………12分

 智能訓(xùn)練練測考系列答案
智能訓(xùn)練練測考系列答案 計算高手系列答案
計算高手系列答案科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
 ,科目B每次考試成績合格的概率均為
,科目B每次考試成績合格的概率均為 .假設(shè)各次考試成績合格與否均互不影響.
.假設(shè)各次考試成績合格與否均互不影響. 率;
率; 棄所有的考試機(jī)會,記他參加考試的次數(shù)為
棄所有的考試機(jī)會,記他參加考試的次數(shù)為 ,求
,求 的數(shù)學(xué)期望E
的數(shù)學(xué)期望E .
.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
 ,動圓
,動圓 過點
過點 且與圓
且與圓 相切,記動圓圓
相切,記動圓圓 的軌跡為
的軌跡為 .
. 的方程;
的方程; 為曲線
為曲線 上任意一點,證明直線
上任意一點,證明直線 與曲線
與曲線 恒有且只有一個公共點.
恒有且只有一個公共點.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
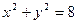 內(nèi)有一點
內(nèi)有一點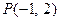 ,
,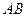 為過點
為過點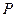 的直線。
的直線。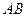 的傾斜角為
的傾斜角為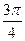 時,求弦
時,求弦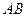 的長
的長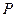 為弦
為弦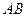 的中點時,求直線
的中點時,求直線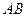 的方程
的方程查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
| A.(x+3)2+(y+2)2=2 | B.(x+3)2+(y+2)2= |
| C.(x+3)2+(y-2)2=2 | D.(x+3)2+(y-2)2= |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com