
已知函數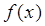 =ax2+(b-8)x-a-ab , 當x
=ax2+(b-8)x-a-ab , 當x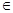 (-∞,-3)
(-∞,-3)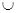 (2,+∞)時,
(2,+∞)時, 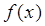 <0,當x
<0,當x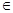 (-3,2)時
(-3,2)時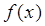 >0 .
>0 .
(1)求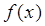 在[0,1]內的值域.
在[0,1]內的值域.
(2)若ax2+bx+c≤0的解集為R,求實數c的取值范圍.
 小學能力測試卷系列答案
小學能力測試卷系列答案科目:高中數學 來源: 題型:022
已知y=Ax2+Bx+C中A, B, C∈{0,1,2,…,9}, 且A, B, C中恰有一個為奇數. 則這樣的二次函數共有__________(A, B, C互不相同).
查看答案和解析>>
科目:高中數學 來源:天津市新人教A版數學2012屆高三單元測試39:微積分基本定理及應用 題型:044
已知y=ax2+bx通過點(1,2),與y=-x2+2x有一個交點x1,且a<0.如下圖所示:

(1)求y=ax2與y=-x2+2x所圍的面積S與a的函數關系.
(2)當a,b為何值時,S取得最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本題總分14分)已知函數![]() =ax2+x-3,g(x)=-x+4lnx
=ax2+x-3,g(x)=-x+4lnx
h(x)=![]() -g(x)
-g(x)
(1)當a=1時,求函數h(x)的極值。
(2)若函數h(x)有兩個極值點,求實數a的取值范圍。
(3)定義:對于函數F(x)和G(x),若存在直線l:y=kx+b,使得對于函數F(x)和
G(x)各自定義域內的任意x,都有F(x)≥kx+b且G(x)≤kx+b成立,則稱直線l:y=kx+b為函數F(x)和G(x)的“隔離直線”。則當a=1時,函數![]() 和g(x)是否存在“隔離直線”。若存在,求出所有的“隔離直線”。若不存在,請說明理由。
和g(x)是否存在“隔離直線”。若存在,求出所有的“隔離直線”。若不存在,請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
已知函數![]() =ax2+(b-8)x-a-ab , 當x
=ax2+(b-8)x-a-ab , 當x![]() (-∞,-3)
(-∞,-3)![]() (2,+∞)時,
(2,+∞)時, ![]() <0,當x
<0,當x![]() (-3,2)時
(-3,2)時![]() >0 .
>0 .
(1)求![]() 在[0,1]內的值域.
在[0,1]內的值域.
(2)若ax2+bx+c≤0的解集為R,求實數c的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com