
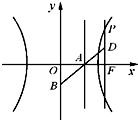
 如圖,已知雙曲線
如圖,已知雙曲線| x2 |
| a2 |
| y2 |
| b2 |
| OD |
| OF |
| OP |
| OM |
| ON |
| OD |
| OF |
| OP |
| b3 |
| a2 |
| b2 |
| a |
| OM |
| ON |
| a2 |
| c |
| b2 |
| a |
| x | ||
|
| y |
| -b |
| b3 |
| a2 |
| b3 |
| a2 |
| OD |
| OF |
| OP |
| b3 |
| a2 |
| b2 |
| a |
| 2b3 |
| a2 |
| b2 |
| a |
| c |
| a |
| ||
| a |
1+(
|
| ||
| 2 |
| x2 |
| 4 |
|
|
| 5 |
| 4 |
| 1 |
| 4 |
| 16k |
| 4k2-1 |
| 20 |
| 4k2-1 |
| OM |
| ON |
| 20(1+k2) |
| 4k2-1 |
| 32k2 |
| 4k2-1 |
| 4k2+16 |
| 4k2-1 |
| 17 |
| 4k2-1 |
| 5 |
| 4 |
| 1 |
| 4 |
| 17 |
| 4k2-1 |
| 17 |
| 4 |
| OM |
| ON |
| 21 |
| 4 |


科目:高中數學 來源: 題型:
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
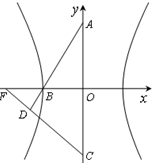 如圖,已知雙曲線x2-
如圖,已知雙曲線x2-| y2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2013•上海)如圖,已知雙曲線C1:
(2013•上海)如圖,已知雙曲線C1:| x2 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源:2013年全國普通高等學校招生統一考試文科數學(上海卷解析版) 題型:填空題
如圖,已知雙曲線C1: ,曲線C2:|y|=|x|+1,P是平面內一點,若存在過點P的直線與C1,C2都有公共點,則稱P為“C1﹣C2型點“
,曲線C2:|y|=|x|+1,P是平面內一點,若存在過點P的直線與C1,C2都有公共點,則稱P為“C1﹣C2型點“

(1)在正確證明C1的左焦點是“C1﹣C2型點“時,要使用一條過該焦點的直線,試寫出一條這樣的直線的方程(不要求驗證);
(2)設直線y=kx與C2有公共點,求證|k|>1,進而證明原點不是“C1﹣C2型點”;
(3)求證:圓x2+y2= 內的點都不是“C1﹣C2型點”
內的點都不是“C1﹣C2型點”
查看答案和解析>>
科目:高中數學 來源:湖北省模擬題 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com