
【題目】如圖所示,在四棱錐P-ABCD中,底面四邊形ABCD是菱形,AC∩BD=O,△PAC是邊長為2的等邊三角形,![]() .
.
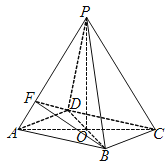
(1)求四棱錐P-ABCD的體積VP-ABCD;
(2)在線段PB上是否存在一點M,使得CM∥平面BDF?如果存在,求![]() 的值,如果不存在,請說明理由.
的值,如果不存在,請說明理由.
【答案】(1)2;(2)![]()
【解析】
(1)證明PO⊥平面ABCD,計算PO,AC,BD,代入體積公式計算;
(2)過C構造平面BCE,使得平面BCE∥BDF,利用三角形的中線的性質得出M的位置.
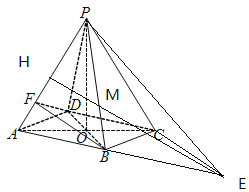
(1)解:∵底面ABCD是菱形,∴O為AC,BD的中點
又∵PA=PC,PB=PD,∴PO⊥AC,PO⊥BD,
∵AC∩BD=O,AC面ABCD,BD面ABCD,
∴PO⊥底面ABCD.
△PAC中,AC=2,∴![]() ,△PBD中,
,△PBD中,![]() ,
,![]() ,
,
![]() .
.
(2)過C作CE∥BD交AB延長線于E,過E作EH∥BF交PA于H,EH與PB交點為M,
∵CE∥BD,BD面BDF,CE面BDF,∴CE∥面BDF,
∵EH∥BF,BF面BDF,EH面BDF,∴EH∥面BDF,
又∵CE∩EH=E,CE面CEM,EH面CEM,
∴面BDF∥面CEM,CM面CEM,
∴CM∥面BDF,
∵BD∥CE,DC∥BE,
∴四邊形BECD為平行四邊形,∴DC=BE=AB,B為AE中點,
∵![]() ∴H為PA中點,
∴H為PA中點,
∴M為中線PB與中線EH的交點,
∴M是△APE的重心,∴![]() =
=![]() .
.


科目:高中數學 來源: 題型:
【題目】已知點![]() 到點
到點![]() 的距離與點
的距離與點![]() 到直線
到直線![]() 的距離相等.
的距離相等.
(1)求點![]() 的軌跡方程;
的軌跡方程;
(2)設點![]() 的軌跡為曲線
的軌跡為曲線![]() ,過點
,過點![]() 且斜率為1的直線與曲線
且斜率為1的直線與曲線![]() 相交于不同的兩點
相交于不同的兩點![]() ,
,![]() ,
,![]() 為坐標原點,求
為坐標原點,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() 經過點
經過點![]() ,且點
,且點![]() 到橢圓的兩焦點的距離之和為
到橢圓的兩焦點的距離之和為![]() .
.
(l)求橢圓![]() 的標準方程;
的標準方程;
(2)若![]() 是橢圓
是橢圓![]() 上的兩個點,線段
上的兩個點,線段![]() 的中垂線
的中垂線![]() 的斜率為
的斜率為![]() 且直線
且直線![]() 與
與![]() 交于點
交于點![]() ,
,![]() 為坐標原點,求證:
為坐標原點,求證:![]() 三點共線.
三點共線.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設甲、乙、丙三個羽毛球協會的運動員人數分別為18,9,18,先采用分層抽樣的方法從這三個協會中抽取5名運動員參加比賽.
(1)求應從這三個協會中分別抽取的運動員人數;
(2)將抽取的5名運動員進行編號,編號分別為![]() ,從這5名運動員中隨機抽取2名參加雙打比賽. 設“編號為
,從這5名運動員中隨機抽取2名參加雙打比賽. 設“編號為![]() 的兩名運動員至少有一人被抽到” 為事件A,求事件A發生的概率.
的兩名運動員至少有一人被抽到” 為事件A,求事件A發生的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com