
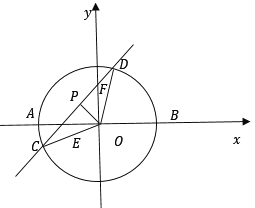
【題目】如圖,圓![]() 與
與![]() 軸交于
軸交于![]() 、
、![]() 兩點,動直線
兩點,動直線![]() (
(![]() )與
)與![]() 軸、
軸、![]() 軸分別交于點
軸分別交于點![]() 、
、![]() ,與圓交于
,與圓交于![]() 、
、![]() 兩點(點
兩點(點![]() 縱坐標大于點
縱坐標大于點![]() 縱坐標).
縱坐標).

(1)若![]() ,點
,點![]() 與點
與點![]() 重合,求點
重合,求點![]() 的坐標;
的坐標;
(2)若![]() ,
,![]() ,求直線
,求直線![]() 將圓分成的劣弧與優弧之比;
將圓分成的劣弧與優弧之比;
(3)若![]() ,設直線
,設直線![]() 、
、![]() 的斜率分別為
的斜率分別為![]() 、
、![]() ,是否存在實數
,是否存在實數![]() 使得
使得![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,說明理由.
的值,若不存在,說明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]()
【解析】
由題意得到![]() ,
,![]() ,
,
(1)由![]() 得
得![]() ,根據點
,根據點![]() 與點
與點![]() 重合,得到
重合,得到![]() 在直線
在直線![]() 上,求出
上,求出![]() ,聯立直線與圓的方程,根據韋達定理,即可求出結果;
,聯立直線與圓的方程,根據韋達定理,即可求出結果;
(2)取![]() 中點為
中點為![]() ,連結
,連結![]() ,由題意得到
,由題意得到![]() ,推出
,推出![]() ,從而求出直線
,從而求出直線![]() ,再求出
,再求出![]() ,進而可求出結果;
,進而可求出結果;
(2)設![]() 、
、![]() ,聯立直線與圓的方程,得到
,聯立直線與圓的方程,得到 ,再由題意得
,再由題意得![]() ,推出
,推出![]() ,求出
,求出![]() 或
或![]() ,根據
,根據![]() 得到
得到![]() ,進而可求出結果.
,進而可求出結果.
因為圓![]() 與
與![]() 軸交于
軸交于![]() 、
、![]() 兩點,所以
兩點,所以![]() ,
,![]() ,
,
(1)由![]() 得
得![]() ,又點
,又點![]() 與點
與點![]() 重合,直線
重合,直線![]() 與圓
與圓![]() 交于
交于![]() 、
、![]() 兩點,
兩點,
所以![]() 在直線
在直線![]() 上,
上,
因此![]() ,所以
,所以![]() ,
,
由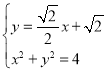 得
得![]() ,所以
,所以![]() ,因此
,因此![]() ,
,
所以![]() ,即
,即 ;
;
(2)取![]() 中點為
中點為![]() ,連結
,連結![]() ,因為
,因為![]() ,所以
,所以![]() 為
為![]() 中點,
中點,
所以![]() ,因此
,因此![]() ,
,
所以直線![]() 的斜率為
的斜率為![]() ,由
,由![]() 得:
得:![]() ,
,
由點到直線距離公式可得:![]() ,又
,又![]() ,
,
所以![]() ,故
,故![]() ,所以
,所以![]() ,
,
因此劣弧![]() 的長度為:
的長度為:![]() ,
,
又圓的周長為:![]() ,
,
所以直線![]() 將圓分成的劣弧與優弧之比為
將圓分成的劣弧與優弧之比為![]() .
.
(3)設![]() 、
、![]() ,因為
,因為![]() ,所以
,所以![]() ,代入圓
,代入圓![]() 可得:
可得:
![]() ,整理得:
,整理得:![]() ,
,
所以 ,
,
又![]() 、
、![]() ,所以
,所以![]() ,
,
又![]() ,
,![]() ,
,
所以 ,
,
即![]() ,即
,即![]() ,
,
整理得:![]() ,解得
,解得![]() 或
或![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() ,
,
即![]() ,即
,即![]() ,
,
所以![]() ,解得
,解得![]() ,所以
,所以![]() .
.


 舉一反三單元同步過關卷系列答案
舉一反三單元同步過關卷系列答案科目:高中數學 來源: 題型:
【題目】已知直線l:4x+3y+10=0,半徑為2的圓C與l相切,圓心C在x軸上且在直線l的右上方.
(1)求圓C的方程;
(2)過點M(1,0)的直線與圓C交于A,B兩點(A在x軸上方),問在x軸正半軸上是否存在定點N,使得x軸平分∠ANB?若存在,請求出點N的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,橢圓C:![]() (a>b>0)的左、右焦點分別為F1,F2,P為橢圓C上一點,且PF2垂直于x軸,連結PF1并延長交橢圓于另一點Q,設
(a>b>0)的左、右焦點分別為F1,F2,P為橢圓C上一點,且PF2垂直于x軸,連結PF1并延長交橢圓于另一點Q,設![]() =λ
=λ![]() .
.

(1)若點P的坐標為(2,3),求橢圓C的方程及λ的值;
(2)若4≤λ≤5,求橢圓C的離心率的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市組織高三全體學生參加計算機操作比賽,等級分為1至10分,隨機調閱了A、B兩所學校各60名學生的成績,得到樣本數據如下:
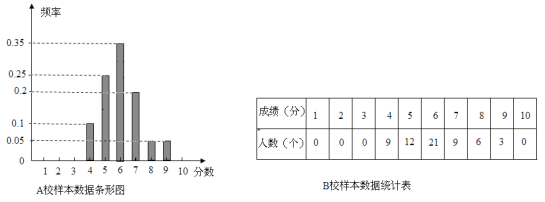
(1)計算兩校樣本數據的均值和方差,并根據所得數據進行比較.
(2)從A校樣本數據成績分別為7分、8分和9分的學生中按分層抽樣方法抽取6人,若從抽取的6人中任選2人參加更高一級的比賽,求這2人成績之和大于或等于15的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以下三個關于圓錐曲線的命題中:
①設![]() 為兩個定點,
為兩個定點,![]() 為非零常數,若
為非零常數,若![]() ,則動點
,則動點![]() 的軌跡是雙曲線;
的軌跡是雙曲線;
②方程![]() 的兩根可分別作為橢圓和雙曲線的離心率;
的兩根可分別作為橢圓和雙曲線的離心率;
③雙曲線![]() 與橢圓
與橢圓![]() 有相同的焦點;
有相同的焦點;
④已知拋物線![]() ,以過焦點的一條弦
,以過焦點的一條弦![]() 為直徑作圓,則此圓與準線相切,其中真命題為__________.(寫出所有真命題的序號)
為直徑作圓,則此圓與準線相切,其中真命題為__________.(寫出所有真命題的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于函數f(x),若存在區間M=[a,b](a<b)使得{y|y=f(x),x∈M}=M,則稱區間M為函數f(x)的一個“穩定區間,給出下列四個函數:
①f(x)![]() ,②f(x)=x3,③f(x)=cos
,②f(x)=x3,③f(x)=cos![]() x,④f(x)=tanx
x,④f(x)=tanx
其中存在“穩定區間”的函數有( )
A.①②③B.②③C.③④D.①④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,一個正方形花圃被分成5份.

(1)若給這5個部分種植花,要求相鄰兩部分種植不同顏色的花,己知現有紅、黃、藍、綠4種顏色不同的花,求有多少種不同的種植方法?
(2)若向這5個部分放入7個不同的盆栽,要求每個部分都有盆栽,問有多少種不同的放法?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com