
【題目】對于函數(shù)f(x),若存在區(qū)間M=[a,b](a<b)使得{y|y=f(x),x∈M}=M,則稱區(qū)間M為函數(shù)f(x)的一個“穩(wěn)定區(qū)間,給出下列四個函數(shù):
①f(x)![]() ,②f(x)=x3,③f(x)=cos
,②f(x)=x3,③f(x)=cos![]() x,④f(x)=tanx
x,④f(x)=tanx
其中存在“穩(wěn)定區(qū)間”的函數(shù)有( )
A.①②③B.②③C.③④D.①④
科目:高中數(shù)學 來源: 題型:
【題目】《九章算術(shù)》中盈不足章中有這樣一則故事:“今有良馬與駑馬發(fā)長安,至齊. 齊去長安三千里. 良馬初日行一百九十三里,日增一十二里;駑馬初日行九十七里,日減二里.” 為了計算每天良馬和駑馬所走的路程之和,設(shè)計框圖如下圖. 若輸出的 ![]() 的值為 350,則判斷框中可填( )
的值為 350,則判斷框中可填( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,圓![]() 與
與![]() 軸交于
軸交于![]() 、
、![]() 兩點,動直線
兩點,動直線![]() (
(![]() )與
)與![]() 軸、
軸、![]() 軸分別交于點
軸分別交于點![]() 、
、![]() ,與圓交于
,與圓交于![]() 、
、![]() 兩點(點
兩點(點![]() 縱坐標大于點
縱坐標大于點![]() 縱坐標).
縱坐標).

(1)若![]() ,點
,點![]() 與點
與點![]() 重合,求點
重合,求點![]() 的坐標;
的坐標;
(2)若![]() ,
,![]() ,求直線
,求直線![]() 將圓分成的劣弧與優(yōu)弧之比;
將圓分成的劣弧與優(yōu)弧之比;
(3)若![]() ,設(shè)直線
,設(shè)直線![]() 、
、![]() 的斜率分別為
的斜率分別為![]() 、
、![]() ,是否存在實數(shù)
,是否存在實數(shù)![]() 使得
使得![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,說明理由.
的值,若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知圓![]() .
.
(1)若圓![]() 的切線在
的切線在![]() 軸、
軸、![]() 軸上的截距相等,求切線方程;
軸上的截距相等,求切線方程;
(2)從圓![]() 外一點
外一點![]() 向該圓引一條切線,切點為
向該圓引一條切線,切點為![]() ,且有
,且有![]() (
(![]() 為坐標原點),求使
為坐標原點),求使![]() 取得最小值時點
取得最小值時點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖所示,近日我漁船編隊在島![]() 周圍海域作業(yè),在島
周圍海域作業(yè),在島![]() 的南偏西20°方向有一個海面觀測站
的南偏西20°方向有一個海面觀測站![]() ,某時刻觀測站發(fā)現(xiàn)有不明船只向我漁船編隊靠近,現(xiàn)測得與
,某時刻觀測站發(fā)現(xiàn)有不明船只向我漁船編隊靠近,現(xiàn)測得與![]() 相距31海里的
相距31海里的![]() 處有一艘海警船巡航,上級指示海警船沿北偏西40°方向,以40海里/小時的速度向島
處有一艘海警船巡航,上級指示海警船沿北偏西40°方向,以40海里/小時的速度向島![]() 直線航行以保護我漁船編隊,30分鐘后到達
直線航行以保護我漁船編隊,30分鐘后到達![]() 處,此時觀測站測得
處,此時觀測站測得![]() 間的距離為21海里.
間的距離為21海里.

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)試問海警船再向前航行多少分鐘方可到島![]() ?
?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=cosx(acosx﹣sinx)![]() (a∈R),且f (
(a∈R),且f (![]() )
)![]() .
.
(1)求a的值;
(2)求f(x)的單調(diào)遞增區(qū)間;
(3)求f(x)在區(qū)間[0,![]() ]上的最小值及對應(yīng)的x的值.
]上的最小值及對應(yīng)的x的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
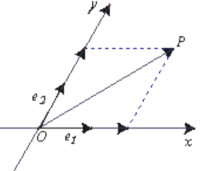
【題目】如圖,設(shè)![]() 是平面內(nèi)相交成
是平面內(nèi)相交成![]() 角的兩條數(shù)軸 ,
角的兩條數(shù)軸 ,![]() 分別是
分別是![]() 軸,
軸,![]() 軸正方向同向的單位向量,若向量
軸正方向同向的單位向量,若向量![]() ,則把有序數(shù)對
,則把有序數(shù)對![]() 叫做向量
叫做向量![]() 在坐標系
在坐標系![]() 中的坐標,假設(shè)
中的坐標,假設(shè)![]() .
.
(1)計算![]() 的大小;
的大小;
(2)設(shè)向量![]() ,若
,若![]() 與
與![]() 共線,求實數(shù)
共線,求實數(shù)![]() 的值;
的值;
(3)是否存在實數(shù)![]() ,使得
,使得![]() 與向量
與向量![]() 垂直,若存在求出
垂直,若存在求出![]() 的值,若不存在請說明理由.
的值,若不存在請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)橢圓M:![]()
![]() 的離心率與雙曲線
的離心率與雙曲線![]() 的離心率互為倒數(shù),且內(nèi)切于圓
的離心率互為倒數(shù),且內(nèi)切于圓![]() 。
。
(1)求橢圓M的方程;
(2)已知![]() ,
,![]() 是橢圓M的下焦點,在橢圓M上是否存在點P,使
是橢圓M的下焦點,在橢圓M上是否存在點P,使![]() 的周長最大?若存在,請求出
的周長最大?若存在,請求出![]() 周長的最大值,并求此時
周長的最大值,并求此時![]() 的面積;若不存在,請說明理由。
的面積;若不存在,請說明理由。
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com