Question

某廠擬生產甲、乙兩種試銷產品，每件銷售收入分別為3千元、2千元． 甲、乙產品都需要在A，B兩種設備上加工，在每臺A、B上加工一件甲所需工時分別為1工時、2工時，加工一件乙所需工時分別為3工時、1工時，A、B兩種設備每月有效使用臺時數為450，問兩種產品各生產多少時，月收入最大值？最大值是多少？．

Answer 1

分析：先設甲、乙兩種產品月產量分別為x、y件，寫出約束條件、目標函數，欲求生產收入最大值的范圍，即求可行域中的最優解，在線性規劃的解答題中建議使用直線平移法求出最優解，即將目標函數看成是一條直線，分析目標函數Z與直線截距的關系，進而求出最優解．注意：最后要將所求最優解還原為實際問題．

解答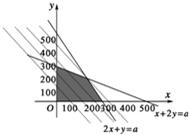：解：設甲、乙兩種產品月的產量分別為x，y件，（1分）
約束條件是 

x+3y≤450 2x+y≤450 x≥0 y≥0

------------（4分）
目標函數是z=3x+2y------------（5分）
由約束條件畫出可行域，如圖．------（8分）
將z=3x+2y它變形為y=-

3

2

x+

z

2

，
這是斜率為-

3

2

、隨z變化的一簇直線．

z

2

是直線在y軸上的截距，當

z

2

最大時z最大，當然直線要與可行域相交，即在滿足約束條件時目標函數取得最大值．
由

x+3y=450 2x+y=450

解得 

x=180 y=90

--------------------（11分）
在這個問題中，使z=3x+2y取得最大值的（x，y）是兩直線2x+y=450與x+3y=450的交點（180，90）．--（10分）∴z=3•×180+2•×90=720（千元）…（13分）
答：每月生產甲180件，生產乙90件月生產收入最大，最大值為72萬元-----（14分）

點評：在解決線性規劃的應用題時，其步驟為：①分析題目中相關量的關系，列出不等式組，即約束條件?②由約束條件畫出可行域?③分析目標函數Z與直線截距之間的關系?④使用平移直線法求出最優解?⑤還原到現實問題中．