
【題目】如圖,設點![]() 是拋物線
是拋物線![]() 的焦點,直線
的焦點,直線![]() 與拋物線
與拋物線![]() 相切于點
相切于點![]() (點
(點![]() 位于第一象限),并與拋物線
位于第一象限),并與拋物線![]() 的準線相交于點
的準線相交于點![]() .過點
.過點![]() 且與直線
且與直線![]() 垂直的直線
垂直的直線![]() 交拋物線
交拋物線![]() 于另一點
于另一點![]() ,交
,交![]() 軸于點
軸于點![]() ,連結
,連結![]() .
.
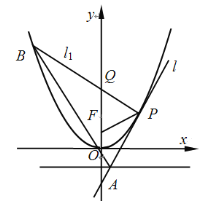
(1)證明:![]() 為等腰三角形;
為等腰三角形;
(2)求![]() 面積的最小值.
面積的最小值.
 學練快車道快樂假期暑假作業新疆人民出版社系列答案
學練快車道快樂假期暑假作業新疆人民出版社系列答案 浙大優學小學年級銜接導與練浙江大學出版社系列答案
浙大優學小學年級銜接導與練浙江大學出版社系列答案 小學暑假作業東南大學出版社系列答案
小學暑假作業東南大學出版社系列答案 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案 波波熊暑假作業江西人民出版社系列答案
波波熊暑假作業江西人民出版社系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,過點
,過點![]() 作平面
作平面![]() 的垂線,垂足為
的垂線,垂足為![]() 與
與![]() 的交點
的交點![]() ,
,![]() 是線段
是線段![]() 的中點.
的中點.
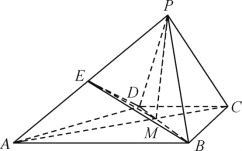
(1)求證:DE//平面![]() ;
;
(2)若四棱錐![]() 的體積為
的體積為![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 為
為![]() 的中點,點
的中點,點![]() ,
,![]() 分別在線段
分別在線段![]() ,
,![]() 上運動(其中
上運動(其中![]() 不與
不與![]() ,
,![]() 重合,
重合,![]() 不與
不與![]() ,
,![]() 重合),且
重合),且![]() ,沿
,沿![]() 將
將![]() 折起,得到三棱錐
折起,得到三棱錐![]() ,則三棱錐
,則三棱錐![]() 體積的最大值為__________;當三棱錐
體積的最大值為__________;當三棱錐![]() 體積最大時,其外接球的表面積的值為_______________.
體積最大時,其外接球的表面積的值為_______________.
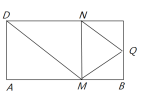
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】用2與0兩個數字排成7位的數碼,其中“20”和“02”各至少出現兩次(如0020020、2020200、0220220等),則這樣的數碼的個數是( )
A.54B.44C.32D.22
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正方體![]() 中,
中,![]() ,
,![]() 分別是棱
分別是棱![]() ,
,![]() 的中點,點
的中點,點![]() 在對角線
在對角線![]() 上運動.當
上運動.當![]() 的面積取得最小值時,點
的面積取得最小值時,點![]() 的位置是( )
的位置是( )

A.線段![]() 的三等分點,且靠近點
的三等分點,且靠近點![]() B.線段
B.線段![]() 的中點
的中點
C.線段![]() 的三等分點,且靠近點
的三等分點,且靠近點![]() D.線段
D.線段![]() 的四等分點,且靠近點
的四等分點,且靠近點![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列![]() (
(![]() )的各項均為正整數,且
)的各項均為正整數,且![]() .若對任意
.若對任意![]() ,存在正整數
,存在正整數![]() 使得
使得![]() ,則稱數列
,則稱數列![]() 具有性質
具有性質![]() .
.
(1)判斷數列![]() 與數列
與數列![]() 是否具有性質
是否具有性質![]() ;(只需寫出結論)
;(只需寫出結論)
(2)若數列![]() 具有性質
具有性質![]() ,且
,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的最小值;
的最小值;
(3)若集合![]() ,且
,且![]() (任意
(任意![]() ,
,![]() ).求證:存在
).求證:存在![]() ,使得從
,使得從![]() 中可以選取若干元素(可重復選取)組成一個具有性質
中可以選取若干元素(可重復選取)組成一個具有性質![]() 的數列.
的數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為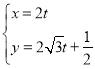 (
(![]() 為參數).以坐標原點為極點,
為參數).以坐標原點為極點,![]() 軸的非負半軸為極軸且取相同的單位長度建立極坐標系,圓
軸的非負半軸為極軸且取相同的單位長度建立極坐標系,圓![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程與圓
的普通方程與圓![]() 的直角坐標方程;
的直角坐標方程;
(2)設動點![]() 在圓
在圓![]() 上,動線段
上,動線段![]() 的中點
的中點![]() 的軌跡為
的軌跡為![]() ,
,![]() 與直線
與直線![]() 交點為
交點為![]() ,且直角坐標系中,
,且直角坐標系中,![]() 點的橫坐標大于
點的橫坐標大于![]() 點的橫坐標,求點
點的橫坐標,求點![]() 的直角坐標.
的直角坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com