【題目】如圖，在正方體
中，
，
分別是棱
，
的中點，點
在對角線
上運動.當
的面積取得最小值時，點的位置是（ ）
A.線段的三等分點，且靠近點
B.線段的中點
C.線段的三等分點，且靠近點
D.線段的四等分點，且靠近點
數學奧賽暑假天天練南京大學出版社系列答案
南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案科目：高中數學 來源： 題型：
【題目】在正方體
中，棱長為2，
分別為棱
的中點，
為底面正方形
內一點（含邊界）且
與面所成角的正切值為
，直線與面
的交點為
，當到
的距離最小時，則四面體
外接球的表面積為___________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】十八大以來，黨中央提出要在2020年實現全面脫貧，為了實現這一目標，國家對“新農合”（新型農村合作醫療）推出了新政，各級財政提高了對“新農合”的補助標準．提高了各項報銷的比例，其中門診報銷比例如下：
表1：新農合門診報銷比例
醫院類別 | 村衛生室 | 鎮衛生院 | 二甲醫院 | 三甲醫院 |
門診報銷比例 | 60% | 40% | 30% | 20% |
根據以往的數據統計，李村一個結算年度門診就診人次情況如下：
表2：李村一個結算年度門診就診情況統計表
醫院類別 | 村衛生室 | 鎮衛生院 | 二甲醫院 | 三甲醫院 |
一個結算年度內各門診就診人次占李村總就診人次的比例 | 70% | 10% | 15% | 5% |
如果一個結算年度每人次到村衛生室、鎮衛生院、二甲醫院、三甲醫院門診平均費用分別為50元、100元、200元、500元．若李村一個結算年度內去門診就診人次為2000人次．
（Ⅰ）李村在這個結算年度內去三甲醫院門診就診的人次中，60歲以上的人次占了80%，從去三甲醫院門診就診的人次中任選2人次，恰好2人次都是60歲以上人次的概率是多少？
（Ⅱ）如果將李村這個結算年度內門診就診人次占全村總就診人次的比例視為概率，求李村這個結算年度每人次用于門診實付費用（報銷后個人應承擔部分）
的分布列與期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，設點
是拋物線
的焦點，直線
與拋物線
相切于點
（點位于第一象限），并與拋物線的準線相交于點
．過點且與直線垂直的直線
交拋物線于另一點
，交
軸于點
，連結
．
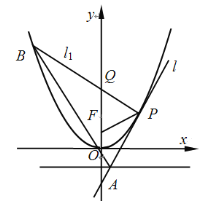
（1）證明：
為等腰三角形；
（2）求
面積的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
，圓
（
為坐標原點）.過點
且斜率為
的直線與圓交于點
，與橢圓
的另一個交點的橫坐標為
.
（1）求橢圓的方程和圓的方程；
（2）過圓上的動點
作兩條互相垂直的直線
，
，若直線的斜率為
且與橢圓相切，試判斷直線與橢圓的位置關系，并說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列結論中正確的個數是（ ）
①在
中，“
”是“
”的必要不充分條件；
②若
，
的最小值為2；
③夾在圓柱的兩個平行截面間的幾何體是圓柱；
④數列
的通項公式為
，則數列的前
項和
．（ ）
A.0B.1C.2D.3
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】科學家為研究對某病毒有效的疫苗，通過小鼠進行毒性和藥效預實驗.已知5只小鼠中有1只患有這種病毒引起的疾病，需要通過化驗血液來確定患病的小鼠.血液化驗結果呈陽性的即為患病小鼠，呈陰性即沒患病.下面是兩種化驗方案：
方案甲：逐個化驗，直到能確定患病小鼠為止.
方案乙：先任取3只，將它們的血液混在一起化驗.若結果呈陽性則表明患病動物為這3只中的1只，然后再逐個化驗，直到能確定患病小鼠為止；若結果呈陰性則在另外2只中任取1只化驗.
（1）求方案甲化驗次數X的分布列；
（2）判斷哪一個方案的效率更高，并說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨著移動互聯網的發展，越來越多的人習慣用手機應用程序（簡稱app）獲取新聞資訊.為了解用戶對某款新聞類app的滿意度，隨機調查了300名用戶，調研結果如表：（單位：人）
青年人 | 中年人 | 老年人 | |
滿意 | 60 | 70 | x |
一般 | 55 | 25 | y |
不滿意 | 25 | 5 | 10 |
（1）從所有參與調研的人中隨機選取1人，估計此人“不滿意”的概率；
（2）從參與調研的青年人和中年人中各隨機選取1人，估計恰有1人“滿意”的概率；
（3）現需從參與調研的老年人中選擇6人作進一步訪談，若在“滿意”、“一般”、“不滿意”的老年人中各取2人，這種抽樣是否合理？說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
