
【題目】已知函數![]() .(
.(![]() 是自然對數的底數)
是自然對數的底數)
(1)求![]() 的單調遞減區間;
的單調遞減區間;
(2)若函數![]() ,證明
,證明![]() 在
在![]() 上只有兩個零點.(參考數據:
上只有兩個零點.(參考數據:![]() )
)
【答案】(1)![]() (k∈Z).(2)見解析.
(k∈Z).(2)見解析.
【解析】
(1)由f'(x)<0得![]() ,利用正弦函數的單調性質可得f(x)的單調遞減區間;
,利用正弦函數的單調性質可得f(x)的單調遞減區間;
(2)依題意可得g'(x)=ex(sinx+cosx)﹣2,分析其單調情況并作出圖象,利用零點存在性定理可得,g(x)在(x1,x2)和(x2,π)內各有一個零點,從而可證得結論成立.
(1)f(x)=exsinx,定義域為R.![]() .
.
由f'(x)<0得![]() ,解得
,解得![]() (k∈Z).
(k∈Z).
∴f(x)的單調遞減區間為![]() (k∈Z).
(k∈Z).
(2)∵g'(x)=ex(sinx+cosx)﹣2,∴g'(x)=2excosx.
∵x∈(0,π),∴當![]() 時,g'(x)>0;當
時,g'(x)>0;當![]() 時,g'(x)<0.
時,g'(x)<0.
∴g'(x)在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,
上單調遞減,
又∵g'(0)=1﹣2<0,![]() ,g'(π)=﹣eπ﹣2<0,
,g'(π)=﹣eπ﹣2<0,
∴g'(x)在(0,π)上圖象大致如右圖.
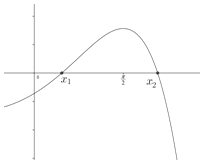
∴![]() ,
,![]() ,使得g'(x1)=0,g'(x2)=0,
,使得g'(x1)=0,g'(x2)=0,
且當x∈(0,x1)或x∈(x2,π)時,g'(x)<0;當x∈(x1,x2)時,g'(x)>0.
∴g(x)在(0,x1)和(x2,π)上單調遞減,在(x1,x2)上單調遞增.
∵g(0)=0,∴g(x1)<0.
∵![]() ,∴g(x2)>0,
,∴g(x2)>0,
又∵g(π)=﹣2π<0,由零點存在性定理得,g(x)在(x1,x2)和(x2,π)內各有一個零點,
∴函數g(x)在(0,π)上有兩個零點.


 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:高中數學 來源: 題型:
【題目】從某居民區隨機抽取10個家庭,獲得第![]() 個家庭的月收入
個家庭的月收入![]() (單位:千元)與月儲蓄
(單位:千元)與月儲蓄![]() (單位:千元)的數據資料,算得
(單位:千元)的數據資料,算得![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求家庭的月儲蓄![]() 對月收入
對月收入![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)若該居民區某家庭月收入為7千元,預測該家庭的月儲蓄.
(附:線性回歸方程![]() 中,
中,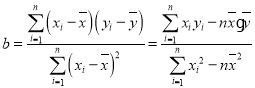 ,其中
,其中![]() ,
,![]() 為樣本平均值.
為樣本平均值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=log2(kx2+4kx+3).①若f(x)的定義域為R,則k的取值范圍是_____;②若f(x)的值域為R,則k的取值范圍是_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
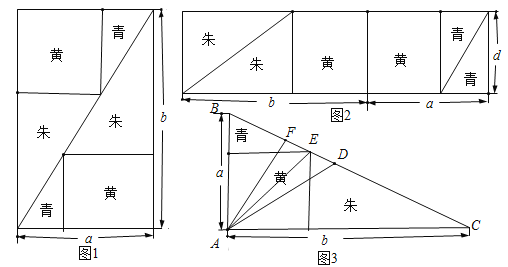
【題目】《九章算術》中“勾股容方”問題:“今有勾五步,股十二步,問勾中容方幾何?”魏晉時期數學家劉徽在其《九章算術注》中利用出入相補原理給出了這個問題的一般解法:如圖1,用對角線將長和寬分別為![]() 和
和![]() 的矩形分成兩個直角三角形,每個直角三角形再分成一個內接正方形(黃)和兩個小直角三角形(朱、青).將三種顏色的圖形進行重組,得到如圖2所示的矩形.該矩形長為
的矩形分成兩個直角三角形,每個直角三角形再分成一個內接正方形(黃)和兩個小直角三角形(朱、青).將三種顏色的圖形進行重組,得到如圖2所示的矩形.該矩形長為![]() ,寬為內接正方形的邊長
,寬為內接正方形的邊長![]() .由劉徽構造的圖形還可以得到許多重要的結論,如圖3.設
.由劉徽構造的圖形還可以得到許多重要的結論,如圖3.設![]() 為斜邊
為斜邊![]() 的中點,作直角三角形
的中點,作直角三角形![]() 的內接正方形對角線
的內接正方形對角線![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() ,則下列推理正確的是( )
,則下列推理正確的是( )
①由圖1和圖2面積相等得![]() ;
;
②由![]() 可得
可得![]() ;
;
③由![]() 可得
可得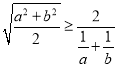 ;
;
④由![]() 可得
可得![]() .
.
A.①②③④B.①②④C.②③④D.①③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若四面體ABCD的三組對棱分別相等,即AB=CD,AC=BD,AD=BC,則下列結論正確的是( )
A.四面體ABCD每組對棱相互垂直
B.四面體ABCD每個面的面積相等
C.從四面體ABCD每個頂點出發的三條棱兩兩夾角之和大于90°且小于180°
D.連接四面體ABCD每組對棱中點的線段相互垂直平分
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于![]() 的說法,正確的是( )
的說法,正確的是( )
A.展開式中的二項式系數之和為2048
B.展開式中只有第6項的二項式系數最大
C.展開式中第6項和第7項的二項式系數最大
D.展開式中第6項的系數最小
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】要得到函數![]() 的圖象,只要將函數
的圖象,只要將函數![]() 的圖象( )
的圖象( )
A.每一點的橫坐標變為原來的![]() 倍(縱坐標不變),再將所得圖象向左平移
倍(縱坐標不變),再將所得圖象向左平移![]() 個長度
個長度
B.每一點的橫坐標變為原來的![]() 倍(縱坐標不變),再將所得圖象向左平移
倍(縱坐標不變),再將所得圖象向左平移![]() 個長度
個長度
C.向左平移![]() 個長度,再將所得圖象每一點的橫坐標變為原來的
個長度,再將所得圖象每一點的橫坐標變為原來的![]() 倍(縱坐標不變)
倍(縱坐標不變)
D.向左平移![]() 個長度,再將所得圖象每一點的橫坐標變為原來的
個長度,再將所得圖象每一點的橫坐標變為原來的![]() 倍(縱坐標不變)
倍(縱坐標不變)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com