
【題目】設(shè)圓![]() 的圓心在
的圓心在![]() 軸的正半軸上,與
軸的正半軸上,與![]() 軸相交于點(diǎn)
軸相交于點(diǎn)![]() ,且直線
,且直線![]() 被圓
被圓![]() 截得的弦長為
截得的弦長為![]() .
.
(1)求圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)設(shè)直線![]() 與圓
與圓![]() 交于
交于![]() 兩點(diǎn),那么以
兩點(diǎn),那么以![]() 為直徑的圓能否經(jīng)過原點(diǎn),若能,請求出直線
為直徑的圓能否經(jīng)過原點(diǎn),若能,請求出直線![]() 的方程;若不能,請說明理由.
的方程;若不能,請說明理由.
【答案】(1)![]() ;(2)能,
;(2)能,![]() 或
或![]() .
.
【解析】
(1)設(shè)圓心![]() ,
,![]() ,半徑為
,半徑為![]() ,由垂徑定理列關(guān)于
,由垂徑定理列關(guān)于![]() 與
與![]() 的方程,結(jié)合點(diǎn)在圓上聯(lián)立求得
的方程,結(jié)合點(diǎn)在圓上聯(lián)立求得![]() 與
與![]() 的值,則圓
的值,則圓![]() 的方程可求;
的方程可求;
(2)設(shè)![]() ,
,![]() ,
,![]() ,
,![]() 是直線
是直線![]() 與圓
與圓![]() 的交點(diǎn),聯(lián)立直線方程與圓的方程,化為關(guān)于
的交點(diǎn),聯(lián)立直線方程與圓的方程,化為關(guān)于![]() 的一元二次方程,利用根與系數(shù)的關(guān)系結(jié)合中點(diǎn)坐標(biāo)公式可得
的一元二次方程,利用根與系數(shù)的關(guān)系結(jié)合中點(diǎn)坐標(biāo)公式可得![]() 的中點(diǎn)
的中點(diǎn)![]() 的坐標(biāo),假如以
的坐標(biāo),假如以![]() 為直徑的圓過原點(diǎn),則
為直徑的圓過原點(diǎn),則![]() ,由此列式求解
,由此列式求解![]() 值,則直線
值,則直線![]() 的方程可求.
的方程可求.
(1)設(shè)圓心![]() ,半徑為
,半徑為![]() ,由垂徑定理得
,由垂徑定理得
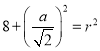 且
且![]()
解得![]() ,
,
∴圓![]() 的方程為
的方程為![]() ;
;
(2)設(shè)![]() 是直線
是直線![]() 與圓
與圓![]() 的交點(diǎn),
的交點(diǎn),
將![]() 代入圓
代入圓![]() 的方程得:
的方程得:![]()
![]()
∴![]() ,
,![]()
∴![]() 的中點(diǎn)為
的中點(diǎn)為![]() .
.
以![]() 為直徑的圓能過原點(diǎn),則
為直徑的圓能過原點(diǎn),則![]() ,
,
∵圓心![]() 到直線
到直線![]() 的距離為
的距離為![]() ,
,
∴![]() .
.
∴![]() ,解得
,解得![]() ,
,
經(jīng)檢驗(yàn)![]() 時(shí),直線
時(shí),直線![]() 與圓
與圓![]() 均相交,
均相交,
∴![]() 的方程為
的方程為![]() 或
或![]() .
.


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某公司全年的純利潤為![]() 元,其中一部分作為獎金發(fā)給
元,其中一部分作為獎金發(fā)給![]() 位職工,獎金分配方案如下首先將職工工作業(yè)績(工作業(yè)績均不相同)從大到小,由1到
位職工,獎金分配方案如下首先將職工工作業(yè)績(工作業(yè)績均不相同)從大到小,由1到![]() 排序,第1位職工得獎金
排序,第1位職工得獎金![]() 元,然后再將余額除以
元,然后再將余額除以![]() 發(fā)給第2位職工,按此方法將獎金逐一發(fā)給每位職工,并將最后剩余部分作為公司發(fā)展基金.
發(fā)給第2位職工,按此方法將獎金逐一發(fā)給每位職工,并將最后剩余部分作為公司發(fā)展基金.
(1)設(shè)![]() 為第
為第![]() 位職工所得獎金額,試求
位職工所得獎金額,試求![]() 并用
并用![]() 和
和![]() 表示
表示![]() (不必證明);
(不必證明);
(2)證明![]() 并解釋此不等式關(guān)于分配原則的實(shí)際意義;
并解釋此不等式關(guān)于分配原則的實(shí)際意義;
(3)發(fā)展基金與![]() 和
和![]() 有關(guān),記為
有關(guān),記為![]() 對常數(shù)
對常數(shù)![]() ,當(dāng)
,當(dāng)![]() 變化時(shí),求
變化時(shí),求![]() .(可用公式
.(可用公式![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
![]() 1
1![]() 當(dāng)
當(dāng)![]() 時(shí),求曲線
時(shí),求曲線![]() 在
在![]() 處的切線方程;
處的切線方程;
![]() 2
2![]() 若
若![]() 是R上的單調(diào)遞增函數(shù),求a的取值范圍;
是R上的單調(diào)遞增函數(shù),求a的取值范圍;
![]() 3
3![]() 若函數(shù)
若函數(shù)![]() 對任意的實(shí)數(shù)
對任意的實(shí)數(shù)![]() ,存在唯一的實(shí)數(shù)
,存在唯一的實(shí)數(shù)![]() ,使得
,使得![]() 成立,求a的值.
成立,求a的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】點(diǎn)P是拋物線![]() 上一動點(diǎn),則點(diǎn)P到點(diǎn)
上一動點(diǎn),則點(diǎn)P到點(diǎn)![]() 的距離與P到直線
的距離與P到直線![]() 的距離和的最小值是( )
的距離和的最小值是( )
A.![]() B.
B.![]() C.3D.
C.3D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() ,為正項(xiàng)數(shù)列
,為正項(xiàng)數(shù)列![]() 的前n項(xiàng)和,且
的前n項(xiàng)和,且![]() .數(shù)列
.數(shù)列![]() 滿足:
滿足:![]() ,
,![]() .
.
(1)求數(shù)列![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)設(shè)![]() ,求數(shù)列
,求數(shù)列![]() 的前
的前![]() 項(xiàng)和
項(xiàng)和![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在梯形ABCD中,AD//BC,∠ABC=![]() ,
,![]() ,∠ADC=
,∠ADC=![]() ,PA⊥平面ABCD且PA=
,PA⊥平面ABCD且PA=![]() .
.
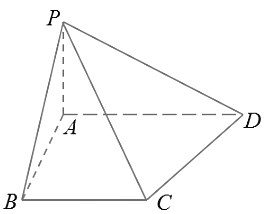
(1)求直線AD到平面PBC的距離;
(2)求出點(diǎn)A到直線PC的距離;
(3)在線段AD上是否存在一點(diǎn)F,使點(diǎn)A到平面PCF的距離為![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)命題p:函數(shù)f(x)=lg(ax2-x+16a)的定義域?yàn)?/span>R;命題q:不等式3x-9x<a對任意x∈R恒成立.
(1)如果p是真命題,求實(shí)數(shù)a的取值范圍;
(2)如果命題“p或q”為真命題且“p且q”為假命題,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】一次考試中,5名同學(xué)的數(shù)學(xué)、物理成績?nèi)绫硭荆?/span>
學(xué)生 |
|
|
|
|
|
數(shù)學(xué) | 89 | 91 | 93 | 95 | 97 |
物理 | 87 | 89 | 89 | 92 | 93 |
![]() 請?jiān)趫D中的直角坐標(biāo)系中作出這些數(shù)據(jù)的散點(diǎn)圖,并求出這些數(shù)據(jù)的回歸方程;
請?jiān)趫D中的直角坐標(biāo)系中作出這些數(shù)據(jù)的散點(diǎn)圖,并求出這些數(shù)據(jù)的回歸方程;
![]() 要從4名數(shù)學(xué)成績在90分以上的同學(xué)中選2名參加一項(xiàng)活動,以X表示選中的同學(xué)的物理成績高于90分的人數(shù),求隨機(jī)變量X的分布列及數(shù)學(xué)期望
要從4名數(shù)學(xué)成績在90分以上的同學(xué)中選2名參加一項(xiàng)活動,以X表示選中的同學(xué)的物理成績高于90分的人數(shù),求隨機(jī)變量X的分布列及數(shù)學(xué)期望![]() .
.
參考公式:線性回歸方程![]() ;,其中
;,其中![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】過拋物線![]() 焦點(diǎn)的直線
焦點(diǎn)的直線![]() 與拋物線交于
與拋物線交于![]() 、
、![]() 兩點(diǎn),與圓
兩點(diǎn),與圓![]() 交于
交于![]() 、
、![]() 兩點(diǎn),若有三條直線滿足
兩點(diǎn),若有三條直線滿足![]() ,則
,則![]() 的取值范圍為______.
的取值范圍為______.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com