
���}Ŀ����ֱ֪��![]() �^�E�A
�^�E�A![]() ���ҽ��c(di��n)���ҽ��E�A��A��B���c(di��n)������AB�����c(di��n)��
���ҽ��c(di��n)���ҽ��E�A��A��B���c(di��n)������AB�����c(di��n)��![]() ��
��
��1����E�A�ķ��̣�
��2���^ԭ�c(di��n)��ֱ��l�c����AB�ཻ���������c(di��n)���ҽ��E�A��C��D���c(di��n)������߅��![]() ��e�����ֵ.
��e�����ֵ.
���𰸡���1��![]() ��2��
��2��![]()
��������
��1����ֱ��![]() �ɵÙE�A�ҽ��c(di��n)������(bi��o)��
�ɵÙE�A�ҽ��c(di��n)������(bi��o)��![]() ,�����c(di��n)
,�����c(di��n)![]() �ɵ�
�ɵ�![]() ,����б�ʹ�ʽ�ɵ�
,����б�ʹ�ʽ�ɵ�![]() ,���c(di��n)
,���c(di��n)![]() �ڙE�A��,�t
�ڙE�A��,�t![]() ,��������,�M(j��n)�����������ɵ�
,��������,�M(j��n)�����������ɵ�![]() ,������⣻
,������⣻
��2���O(sh��)ֱ��![]() ,�c(di��n)
,�c(di��n)![]() ��ֱ��
��ֱ��![]() �ľ��x��
�ľ��x��![]() ,�t��߅�ε���e��
,�t��߅�ε���e��![]() ,��
,��![]() ����E�A����,���������L��ʽ���
����E�A����,���������L��ʽ���![]() ,�����c(di��n)��ֱ�����x���
,�����c(di��n)��ֱ�����x���![]() ,����(j��)ֱ��l�c����AB���������c(di��n)���ཻ,�ɵ�
,����(j��)ֱ��l�c����AB���������c(di��n)���ཻ,�ɵ�![]() ,��
,��![]() ,�M(j��n)������QԪ,�ɶ��κ���(sh��)���|(zh��)�����ֵ����.
,�M(j��n)������QԪ,�ɶ��κ���(sh��)���|(zh��)�����ֵ����.
��1��ֱ��![]() �cx�S�����c(di��n)
�cx�S�����c(di��n)![]() ,���ԙE�A�ҽ��c(di��n)������(bi��o)��
,���ԙE�A�ҽ��c(di��n)������(bi��o)��![]() ,��
,��![]() ,
,
��?y��n)龀��AB�����c(di��n)��![]() ,
,
�O(sh��)![]() ,�t
,�t![]() ,��
,��![]() ,
,
��![]() ,����ɵ�
,����ɵ�![]() ,
,
�t![]() ,��
,��![]()
��![]() ,
,
����![]() ,
,
��˙E�A�ķ��̞�![]() .
.
��2���ɣ�1��(li��n)��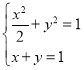 ,���
,���![]() ��
��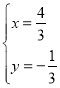 ,
,
������![]() ,��ֱ֪��l��б�ʴ���,
,��ֱ֪��l��б�ʴ���,
�O(sh��)ֱ��![]() ,����
,����![]() ,��
,��![]() ,
,
���![]() ��
��![]() ,
,
�O(sh��)![]() ,�t
,�t![]() ,
,
�t![]() ,
,
��?y��n)?/span>![]() ��ֱ��
��ֱ��![]() �ľ��x�քe��
�ľ��x�քe��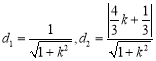 ,
,
����ֱ��l�c����AB���������c(di��n)���ཻ,����![]() ,��
,��![]() ,
,
����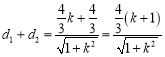 ,
,
��߅��![]() ����e
����e![]() ,
,
��![]() ,
,![]() ,�t
,�t![]() ,
,
����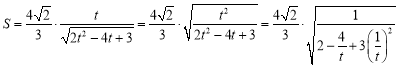 ,
,
��(d��ng)![]() ,��
,��![]() �r,
�r,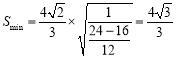 ��
��
�����߅��![]() ��e�����ֵ��
��e�����ֵ��![]() .
.


 һ�����}�����}��ϵ�д�
һ�����}�����}��ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij�мs��20�fס�������˹�(ji��)�s��Դ���M���_���A��늃r���ƶȣ����ƶ�ס������������R��ֵ![]() ����ijס��ij������������^
����ijס��ij������������^![]() �ȣ��t��ƽ�r����ԭ�r��0.5����λ��Ԫ/�ȣ�Ӌ(j��)�M(f��i)����ij����������^
�ȣ��t��ƽ�r����ԭ�r��0.5����λ��Ԫ/�ȣ�Ӌ(j��)�M(f��i)����ij����������^![]() �ȣ��t�������ְ��h�r
�ȣ��t�������ְ��h�r![]() ����λ��Ԫ/�ȣ�Ӌ(j��)�M(f��i)��δ�������ְ�ƽ�rӋ(j��)�M(f��i).��_��
����λ��Ԫ/�ȣ�Ӌ(j��)�M(f��i)��δ�������ְ�ƽ�rӋ(j��)�M(f��i).��_��![]() ��ֵ���S�C(j��)�{(di��o)����ԓ��100��������������y(t��ng)Ӌ(j��)������õ���D��ʾ���l�ʷֲ�ֱ���D.����(j��)�l�ʷֲ�ֱ���D��������}��ͬһ�M��(sh��)��(j��)��ԓ�^(q��)�g�����c(di��n)ֵ��������.
��ֵ���S�C(j��)�{(di��o)����ԓ��100��������������y(t��ng)Ӌ(j��)������õ���D��ʾ���l�ʷֲ�ֱ���D.����(j��)�l�ʷֲ�ֱ���D��������}��ͬһ�M��(sh��)��(j��)��ԓ�^(q��)�g�����c(di��n)ֵ��������.
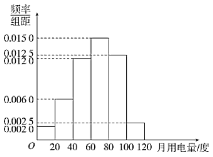
��1����ԓ��Ӌ(j��)��ȫ��70%��ס�������A��늃r�����_ǰ���U�{����M(f��i)��׃�����R��ֵ![]() ��
��
��2���ڣ�1���ėl���£��ٶ����_���A��늃r��֮���������δ�_(d��)![]() �ȵ�ס����������ֲ�׃������������^
�ȵ�ס����������ֲ�׃������������^![]() �ȵ�ס����(ji��)ʡ��������������60%��ԇ��Ӌ(j��)ȫ��ÿ�¹�(ji��)�s�����.
�ȵ�ס����(ji��)ʡ��������������60%��ԇ��Ӌ(j��)ȫ��ÿ�¹�(ji��)�s�����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ijͬ�W(xu��)���Ƴɿ���(y��u)�������ꅢ���˔�(sh��)�W(xu��)�����������W(xu��)������4�T�W(xu��)�Ƹ�ِ����֪ԓͬ�W(xu��)��(sh��)�W(xu��)�@һ�Ȫ��ĸ��ʞ�![]() �����������W(xu��)������@һ�Ȫ��ĸ��ʶ���
�����������W(xu��)������@һ�Ȫ��ĸ��ʶ���![]() �������T�W(xu��)���Ƿ�@һ�Ȫ����(d��)����
�������T�W(xu��)���Ƿ�@һ�Ȫ����(d��)����
��1����ԓͬ�W(xu��)������һ�T�W(xu��)�ƫ@��һ�Ȫ��ĸ��ʣ�
��2�����S�C(j��)׃��![]() ��ʾԓͬ�W(xu��)�@��һ�Ȫ��Ŀ���(sh��)����
��ʾԓͬ�W(xu��)�@��һ�Ȫ��Ŀ���(sh��)����![]() �ĸ��ʷֲ��͔�(sh��)�W(xu��)����
�ĸ��ʷֲ��͔�(sh��)�W(xu��)����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D,��֪�L����![]() ��,
��,![]() ,
,![]() ��
��![]() �����c(di��n). ��
�����c(di��n). ��![]() ��
��![]() ����,ʹ��ƽ��
����,ʹ��ƽ��![]() ƽ��
ƽ��![]() .
.
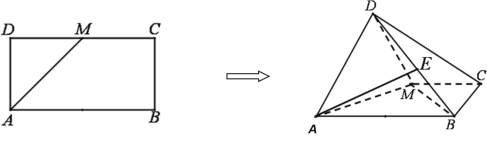
(1)���C:![]() .
.
(2)�c(di��n)![]() �Ǿ���
�Ǿ���![]() �ϵ�һ���c(di��n),��(d��ng)�����
�ϵ�һ���c(di��n),��(d��ng)�����![]() ��С��
��С��![]() �r,ԇ�_���c(di��n)
�r,ԇ�_���c(di��n)![]() ��λ��.
���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
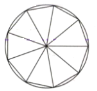
���}Ŀ������(�s��Ԫ225��-295��)��κ�x���g����Ĕ�(sh��)�W(xu��)�ң��Ї��ŵ䔵(sh��)�W(xu��)��Փ�ĵ����֮һ���ڸ�A�g(sh��)������ģ�����֮����(x��)����ʧ���٣���֮�ָ�����ڲ��ɸ�t�c�A�ܺ��w���o��ʧ�������@��ҕ���Ї��Ŵ��O���^��ļ�������A�g(sh��)�ĺ���˼���nj�һ���A�ă�(n��i)����n߅�εȷֳ�n������������(��D��ʾ)����(d��ng)n׃�úܴ�r���@n�����������ε���e֮�ͽ��Ƶ��ڈA����e���\(y��n)�ø�A�g(sh��)��˼�룬�õ�![]() �Ľ���ֵ�飨 ��
�Ľ���ֵ�飨 ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�A��![]() ���Ă���c(di��n)���ɵ���߅�ε���e��
���Ă���c(di��n)���ɵ���߅�ε���e��![]() ��ԭ�c(di��n)��ֱ��
��ԭ�c(di��n)��ֱ��![]() �ľ��x��
�ľ��x��![]() .
.
��1����E�A![]() �ķ��̣�
�ķ��̣�
��2����֪���c(di��n)![]() ���Ƿ�����^
���Ƿ�����^![]() ��ֱ��
��ֱ��![]() ��ʹ
��ʹ![]() �c�E�A
�c�E�A![]() ����
����![]() ��
��![]() ���c(di��n)������
���c(di��n)������![]() ��ֱ���ĈA�^�E�A
��ֱ���ĈA�^�E�A![]() ������c(di��n)�������ڣ����
������c(di��n)�������ڣ����![]() �ķ��̣��������ڣ�Ո�f������.
�ķ��̣��������ڣ�Ո�f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪���タ![]() �Ľ��c(di��n)��
�Ľ��c(di��n)��![]() ���c(di��n)
���c(di��n)![]() �ǒ��タ
�ǒ��タ![]() ������һ�c(di��n)����
������һ�c(di��n)����![]() ��ֱ�����A
��ֱ�����A![]() .
.
��1�����A![]() �c����(bi��o)
�c����(bi��o)![]() �S��λ���P(gu��n)ϵ�����C����ĽY(ji��)Փ��
�S��λ���P(gu��n)ϵ�����C����ĽY(ji��)Փ��
��2���O(sh��)ֱ��![]() �c���タ
�c���タ![]() ����
����![]() ��
��![]() ����
����![]() ����
����![]() ����e��
����e��![]() ����ֱ��
����ֱ��![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D���������F![]() �У�
�У�![]() ���������Σ���߅��ABCD��ֱ�����Σ�
���������Σ���߅��ABCD��ֱ�����Σ�![]() //
//![]() ��ƽ��
��ƽ��![]() ƽ��ABCD���c(di��n)E��F�քe��AD��CP�����c(di��n)��
ƽ��ABCD���c(di��n)E��F�քe��AD��CP�����c(di��n)��![]() .
.
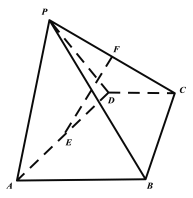
��1���C����ֱ��![]() //ƽ��PAB��
//ƽ��PAB��
��2����ֱ��EF�cƽ��PBC���ɽǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ֱ������(bi��o)ϵ![]() �У��Aб�Ǟ�
�У��Aб�Ǟ�![]() ��ֱ��
��ֱ��![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�![]() ��
��![]() �酢��(sh��)����������(bi��o)ԭ�c(di��n)
�酢��(sh��)����������(bi��o)ԭ�c(di��n)![]() ��O�c(di��n)��
��O�c(di��n)��![]() �S�ķ�ؓ(f��)���S��O�S�����O����(bi��o)ϵ������
�S�ķ�ؓ(f��)���S��O�S�����O����(bi��o)ϵ������![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() .
.
��1����![]() ����ֱ��
����ֱ��![]() �ĘO����(bi��o)���̣�
�ĘO����(bi��o)���̣�
��2����ֱ��![]() ��б�ʞ�
��б�ʞ�![]() ��ֱ��
��ֱ��![]() �c����
�c����![]() �ཻ��
�ཻ��![]() ���c(di��n)���c(di��n)
���c(di��n)���c(di��n)![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com