
【題目】如圖,在四棱錐![]() 中,
中,![]() 為正三角形,四邊形ABCD為直角梯形,
為正三角形,四邊形ABCD為直角梯形,![]() //
//![]() ,平面
,平面![]() 平面ABCD,點E,F分別為AD,CP的中點,
平面ABCD,點E,F分別為AD,CP的中點,![]() .
.
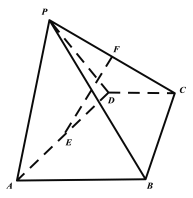
(1)證明:直線![]() //平面PAB;
//平面PAB;
(2)求直線EF與平面PBC所成角的正弦值.
【答案】(1)證明見詳解;(2)![]() .
.
【解析】
(1)取![]() 中點為
中點為![]() ,構造過
,構造過![]() 的平面
的平面![]() ,由面面平行推證線面平行即可;
,由面面平行推證線面平行即可;
(2)取![]() 中點為
中點為![]() ,過
,過![]() 作
作![]() ,找出二面角的平面角,再解三角形即可.
,找出二面角的平面角,再解三角形即可.
(1)取![]() 中點為
中點為![]() ,連接
,連接![]() ,如下圖所示:
,如下圖所示:
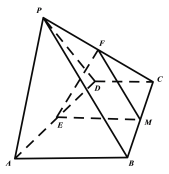
在![]() 中,
中,
因為![]() 分別是
分別是![]() 兩邊的中點,
兩邊的中點,
故可得![]() //
//![]() ;
;
在梯形![]() 中,
中,
因為![]() 分別是兩腰
分別是兩腰![]() 的中點,
的中點,
故可得![]() //
//![]() ;
;
又因為![]() 平面
平面![]() ,且
,且![]() ,
,
![]() 平面
平面![]() ,且
,且![]() ,
,
故可得平行![]() //
//![]() ,
,
又因為![]() 平面
平面![]() ,
,
故可得![]() //平面
//平面![]() ,即證.
,即證.
(2)取![]() 中點為
中點為![]() ,連接
,連接![]() ,
,
過![]() 作
作![]() ,連接
,連接![]() ,如下圖所示:
,如下圖所示:
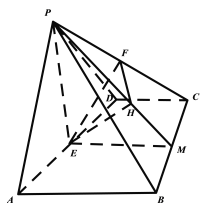
因為![]() 是等邊三角形,且
是等邊三角形,且![]() 為
為![]() 中點,
中點,
故可得![]() ;
;
因為平面![]() 平面
平面![]() ,且兩平面交于
,且兩平面交于![]() ,
,
故可得![]() 平面
平面![]() .
.
又因為![]() 平面
平面![]() ,
,
故可得![]() ;
;
又因為梯形![]() 是直角梯形,
是直角梯形,![]() //
//![]() ,
,
故可得![]() ;
;
又因為![]() 平面
平面![]() ,且交于點
,且交于點![]() ,
,
故可得![]() 平面
平面![]() ,又因為
,又因為![]() 平面
平面![]() ,
,
故可得![]() ;又
;又![]() ,
,
且![]() 平面
平面![]() ,且交于點
,且交于點![]() ,
,
故可得![]() 平面
平面![]() ,則
,則![]() 即為所求線面角.
即為所求線面角.
在梯形![]() 中,
中,
因為![]() ,且
,且![]()
故可得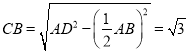 ;
;
在![]() 中,
中,
![]() ;
;![]() ;
;
故可得斜邊![]() 上的高線
上的高線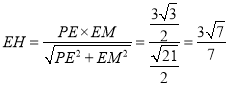 ;
;
在![]() 中,
中,
![]() ;
;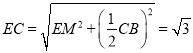 ;
;
故可得斜邊![]() 上的中線
上的中線![]() ;
;
綜上所述:在![]() 中,
中,
![]() ,
,![]() ,
,
故可得![]() .
.
故直線EF與平面PBC所成角的正弦值為![]() .
.


 小天才課時作業系列答案
小天才課時作業系列答案 一課四練系列答案
一課四練系列答案 黃岡小狀元滿分沖刺微測驗系列答案
黃岡小狀元滿分沖刺微測驗系列答案 新輔教導學系列答案
新輔教導學系列答案 陽光同學一線名師全優好卷系列答案
陽光同學一線名師全優好卷系列答案科目:高中數學 來源: 題型:
【題目】已知極點與直角坐標系的原點重合,極軸與![]() 軸的正半軸重合,曲線
軸的正半軸重合,曲線![]() 的極坐標方程是
的極坐標方程是![]() ,直線
,直線![]() 的參數方程是
的參數方程是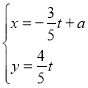 (
(![]() 為參數).
為參數).
(1)若![]() ,
,![]() 是圓
是圓![]() 上一動點,求點
上一動點,求點![]() 到直線
到直線![]() 的距離
的距離![]() 的最小值和最大值;
的最小值和最大值;
(2)直線![]() 與
與![]() 關于原點對稱,且直線
關于原點對稱,且直線![]() 截曲線
截曲線![]() 的弦長等于
的弦長等于![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 過橢圓
過橢圓![]() 的右焦點,且交橢圓于A,B兩點,線段AB的中點是
的右焦點,且交橢圓于A,B兩點,線段AB的中點是![]() ,
,
(1)求橢圓的方程;
(2)過原點的直線l與線段AB相交(不含端點)且交橢圓于C,D兩點,求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 是拋物線
是拋物線![]() :
:![]() 的焦點,點
的焦點,點![]() 為拋物線
為拋物線![]() 的對稱軸與其準線的交點,過
的對稱軸與其準線的交點,過![]() 作拋物線
作拋物線![]() 的切線,切點為
的切線,切點為![]() ,若點
,若點![]() 恰好在以
恰好在以![]() ,
,![]() 為焦點的雙曲線上,則雙曲線的離心率為( )
為焦點的雙曲線上,則雙曲線的離心率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】環境問題是當今世界共同關注的問題,我國環保總局根據空氣污染指數![]() 濃度,制定了空氣質量標準:
濃度,制定了空氣質量標準:
空氣污染質量 |
|
|
|
|
|
|
空氣質量等級 | 優 | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴重污染 |
某市政府為了打造美麗城市,節能減排,從2010年開始考查了連續六年11月份的空氣污染指數,繪制了頻率分布直方圖,經過分析研究,決定從2016年11月1日起在空氣質量重度污染和嚴重污染的日子對機動車輛限號出行,即車牌尾號為單號的車輛單號出行,車牌尾號為雙號的車輛雙號出行(尾號為字母的,前13個視為單號,后13個視為雙號).
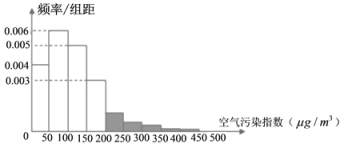
(1)某人計劃11月份開車出行,求因空氣污染被限號出行的概率;
(2)該市環保局為了調查汽車尾氣排放對空氣質量的影響,對限行三年來的11月份共90天的空氣質量進行統計,其結果如表:
空氣質量 | 優 | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴重污染 |
天數 | 16 | 39 | 18 | 10 | 5 | 2 |
根據限行前六年180天與限行后90天的數據,計算并填寫![]() 列聯表,并回答是否有
列聯表,并回答是否有![]() 的把握認為空氣質量的優良與汽車尾氣的排放有關.
的把握認為空氣質量的優良與汽車尾氣的排放有關.
空氣質量優良 | 空氣質量污染 | 合計 | |
限行前 | |||
限行后 | |||
合計 |
參考數據:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 其中
其中![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】己知函數![]() 在
在![]() 處的切線方程為
處的切線方程為![]() ,函數
,函數![]() .
.
(1)求函數![]() 的解析式;
的解析式;
(2)求函數![]() 的極值;
的極值;
(3)設![]() (
(![]() 表示p,q中的最小值),若
表示p,q中的最小值),若![]() 在
在![]() 上恰有三個零點,求實數k的取值范圍.
上恰有三個零點,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】每逢節日,電商之間的價格廝殺已經不是什么新鮮事,今年的6月18日也不例外.某電商在6月18日之后,隨機抽取100名顧客進行回訪,按顧客的年齡分成6組,得到如下頻數分布表:
顧客年齡 |
|
|
|
|
|
|
頻數 | 4 | 24 | 32 | 20 | 16 | 4 |
(1)在下表中作出這些數據的頻率分布直方圖;
(2)用分層抽樣的方法從這100名顧客中抽取25人,再從抽取的25人中隨機抽取2人,求年齡在![]() 內的顧客人數
內的顧客人數![]() 的分布列、數學期望.
的分布列、數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com