
【題目】已知拋物線![]() 的焦點為
的焦點為![]() ,點
,點![]() 是拋物線
是拋物線![]() 上任意一點,以
上任意一點,以![]() 為直徑作圓
為直徑作圓![]() .
.
(1)判斷圓![]() 與坐標
與坐標![]() 軸的位置關系,并證明你的結論;
軸的位置關系,并證明你的結論;
(2)設直線![]() 與拋物線
與拋物線![]() 交于
交于![]() ,
,![]() ,且
,且![]() ,若
,若![]() 的面積為
的面積為![]() ,求直線
,求直線![]() 的方程.
的方程.
科目:高中數學 來源: 題型:
【題目】給出如下四個命題:①若“p且![]() ”為假命題,則p、q均為假命題;②命題“若a>b,則
”為假命題,則p、q均為假命題;②命題“若a>b,則![]() ”的否命題為“若a≤b,則
”的否命題為“若a≤b,則![]() ”;③“x∈R,
”;③“x∈R,![]() 的否定是“
的否定是“![]() ”;④在△ABC中,“A>B”是“
”;④在△ABC中,“A>B”是“![]() ”的充要條件;其中正確的命題的個數是( )
”的充要條件;其中正確的命題的個數是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 過橢圓
過橢圓![]() 的右焦點,且交橢圓于A,B兩點,線段AB的中點是
的右焦點,且交橢圓于A,B兩點,線段AB的中點是![]() ,
,
(1)求橢圓的方程;
(2)過原點的直線l與線段AB相交(不含端點)且交橢圓于C,D兩點,求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() ’(
’(![]() 為參數).以坐標原點為極點,
為參數).以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 和
和![]() 的直角坐標方程;
的直角坐標方程;
(2)已知直線![]() 與
與![]() 軸交于點
軸交于點![]() ,且與曲線
,且與曲線![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 是拋物線
是拋物線![]() :
:![]() 的焦點,點
的焦點,點![]() 為拋物線
為拋物線![]() 的對稱軸與其準線的交點,過
的對稱軸與其準線的交點,過![]() 作拋物線
作拋物線![]() 的切線,切點為
的切線,切點為![]() ,若點
,若點![]() 恰好在以
恰好在以![]() ,
,![]() 為焦點的雙曲線上,則雙曲線的離心率為( )
為焦點的雙曲線上,則雙曲線的離心率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】環境問題是當今世界共同關注的問題,我國環保總局根據空氣污染指數![]() 濃度,制定了空氣質量標準:
濃度,制定了空氣質量標準:
空氣污染質量 |
|
|
|
|
|
|
空氣質量等級 | 優 | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴重污染 |
某市政府為了打造美麗城市,節能減排,從2010年開始考查了連續六年11月份的空氣污染指數,繪制了頻率分布直方圖,經過分析研究,決定從2016年11月1日起在空氣質量重度污染和嚴重污染的日子對機動車輛限號出行,即車牌尾號為單號的車輛單號出行,車牌尾號為雙號的車輛雙號出行(尾號為字母的,前13個視為單號,后13個視為雙號).
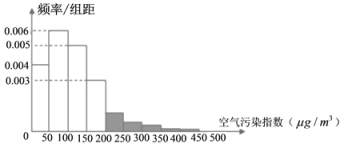
(1)某人計劃11月份開車出行,求因空氣污染被限號出行的概率;
(2)該市環保局為了調查汽車尾氣排放對空氣質量的影響,對限行三年來的11月份共90天的空氣質量進行統計,其結果如表:
空氣質量 | 優 | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴重污染 |
天數 | 16 | 39 | 18 | 10 | 5 | 2 |
根據限行前六年180天與限行后90天的數據,計算并填寫![]() 列聯表,并回答是否有
列聯表,并回答是否有![]() 的把握認為空氣質量的優良與汽車尾氣的排放有關.
的把握認為空氣質量的優良與汽車尾氣的排放有關.
空氣質量優良 | 空氣質量污染 | 合計 | |
限行前 | |||
限行后 | |||
合計 |
參考數據:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 其中
其中![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】己知函數![]() 在
在![]() 處的切線方程為
處的切線方程為![]() ,函數
,函數![]() .
.
(1)求函數![]() 的解析式;
的解析式;
(2)求函數![]() 的極值;
的極值;
(3)設![]() (
(![]() 表示p,q中的最小值),若
表示p,q中的最小值),若![]() 在
在![]() 上恰有三個零點,求實數k的取值范圍.
上恰有三個零點,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率
的離心率![]() ,且橢圓過點
,且橢圓過點![]()
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設直線![]() 與
與![]() 交于
交于![]() 、
、![]() 兩點,點
兩點,點![]() 在橢圓
在橢圓![]() 上,
上,![]() 是坐標原點,若
是坐標原點,若![]() ,判定四邊形
,判定四邊形![]() 的面積是否為定值?若為定值,求出該定值;如果不是,請說明理由.
的面積是否為定值?若為定值,求出該定值;如果不是,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com