
分析 (Ⅰ)由題意可知:數列{an}為公比為2的等比數列,則a3=4a1,a2=2a1,由a1、a2+1、a3成等差數列,則2(2a1+1)=a1+4a1,即可求得a1=2,由等比數列的通項公式,即可求得{an}的通項公式;
(Ⅱ)令bn=log2an=n,則數列{bn}是以1為首項,以1為公差的等差數列,數列{log2an}的前n項和為Sn,Sn=$\frac{n(n+1)}{2}$,由不等式Sn>45,即n2+n-90>0即可求得最小正整數n的值.
解答 解:(Ⅰ)由數列{an}滿足an+1=2an,
∴數列{an}為公比為2的等比數列,
由已知:a1、a2+1、a3成等差數列,即2(a2+1)=a1+a3,
由a3=4a1,a2=2a1,
∴2(2a1+1)=a1+4a1,解得:a1=2,
由等比數列通項公式可知:an=a1•2n-1=2n,
∴數列{an}的通項公式an=2n;
(Ⅱ)令bn=log2an=n,
當n=1時,b1=1,
當n≥2時,bn-bn-1=1,
∴數列{bn}是以1為首項,以1為公差的等差數列,
∴數列{log2an}的前n項和為Sn,Sn=$\frac{n(n+1)}{2}$,
由不等式Sn>45,即n2+n-90>0
解得:n>9,
使不等式Sn>45成立的最小正整數n的值10.
點評 本題考查等差數列的性質,等比數列通項公式,考查對數函數的運算性質,考查數列與不等式的綜合應用,考查計算能力,屬于中檔題.


科目:高中數學 來源: 題型:解答題
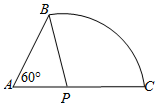 某柱體實心銅制零件的截面邊長是長度為55毫米線段AB和88毫米的線段AC以及圓心為P,半徑為PB的一段圓弧BC構成,其中∠BAC=60°.
某柱體實心銅制零件的截面邊長是長度為55毫米線段AB和88毫米的線段AC以及圓心為P,半徑為PB的一段圓弧BC構成,其中∠BAC=60°.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,在圓錐PO中,已知PO=$\sqrt{2}$,⊙O 的直徑AB=2,C是弧$\widehat{AB}$的中點,D為AC的中點.
如圖,在圓錐PO中,已知PO=$\sqrt{2}$,⊙O 的直徑AB=2,C是弧$\widehat{AB}$的中點,D為AC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | x=$\frac{π}{12}$ | B. | x=-$\frac{π}{12}$ | C. | x=$\frac{π}{6}$ | D. | x=-$\frac{π}{6}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com