
【題目】已知函數(shù)![]() ,其中
,其中![]() 為常數(shù).
為常數(shù).
(1)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)若![]() 存在兩個(gè)極值點(diǎn)
存在兩個(gè)極值點(diǎn)![]() ,求證:無(wú)論實(shí)數(shù)
,求證:無(wú)論實(shí)數(shù)![]() 取什么值都有
取什么值都有![]() .
.
【答案】(1)當(dāng)![]() 時(shí),
時(shí),![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞增;
上單調(diào)遞增;
當(dāng)![]() 時(shí),
時(shí),![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增;
上單調(diào)遞增;
(2)見(jiàn)解析.
【解析】試題分析: (1)先求導(dǎo)數(shù),研究導(dǎo)函數(shù)在定義域上零點(diǎn)情況,本題實(shí)質(zhì)研究![]() 在
在![]() 上零點(diǎn)情況:當(dāng)方程無(wú)根時(shí),函數(shù)單調(diào)遞增;當(dāng)方程有兩個(gè)相等實(shí)根時(shí),函數(shù)單調(diào)遞增;當(dāng)方程有兩個(gè)不等實(shí)根時(shí),比較兩根與定義區(qū)間之間關(guān)系,再確定單調(diào)區(qū)間,(2)先由(1)知
上零點(diǎn)情況:當(dāng)方程無(wú)根時(shí),函數(shù)單調(diào)遞增;當(dāng)方程有兩個(gè)相等實(shí)根時(shí),函數(shù)單調(diào)遞增;當(dāng)方程有兩個(gè)不等實(shí)根時(shí),比較兩根與定義區(qū)間之間關(guān)系,再確定單調(diào)區(qū)間,(2)先由(1)知![]() ,且兩個(gè)極值點(diǎn)
,且兩個(gè)極值點(diǎn)![]() 滿(mǎn)足
滿(mǎn)足![]() .再代入化簡(jiǎn)
.再代入化簡(jiǎn)![]() 得
得![]() ,利用導(dǎo)數(shù)研究
,利用導(dǎo)數(shù)研究![]() 單調(diào)性,最后根據(jù)單調(diào)性證明不等式.
單調(diào)性,最后根據(jù)單調(diào)性證明不等式.
試題解析:(1)函數(shù)的定義域?yàn)?/span>![]() .
.
![]() ,記
,記![]() ,判別式
,判別式![]() .
.
①當(dāng)![]() 即
即![]() 時(shí),
時(shí),![]() 恒成立,
恒成立,![]() ,所以
,所以![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞增.
上單調(diào)遞增.
②當(dāng)![]() 或
或![]() 時(shí),方程
時(shí),方程![]() 有兩個(gè)不同的實(shí)數(shù)根
有兩個(gè)不同的實(shí)數(shù)根![]() ,記
,記![]() ,
,![]() ,顯然
,顯然![]()
(ⅰ)若![]() ,
,![]() 圖象的對(duì)稱(chēng)軸
圖象的對(duì)稱(chēng)軸![]() ,
,![]() .
.
兩根![]() 在區(qū)間
在區(qū)間![]() 上,可知當(dāng)
上,可知當(dāng)![]() 時(shí)函數(shù)
時(shí)函數(shù)![]() 單調(diào)遞增,
單調(diào)遞增,![]() ,所以
,所以![]() ,所以
,所以![]() 在區(qū)間
在區(qū)間![]() 上遞增.
上遞增.
(ⅱ)若![]() ,則
,則![]() 圖象的對(duì)稱(chēng)軸
圖象的對(duì)稱(chēng)軸![]() ,
,![]() .,所以
.,所以![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí),![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 上單調(diào)遞減.當(dāng)
上單調(diào)遞減.當(dāng)![]() 或
或![]() 時(shí),
時(shí),![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 上單調(diào)遞增.
上單調(diào)遞增.
綜上,當(dāng)![]() 時(shí),
時(shí),![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞增;當(dāng)
上單調(diào)遞增;當(dāng)![]() 時(shí),
時(shí),![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增.
上單調(diào)遞增.
(2)由(1)知當(dāng)![]() 時(shí),
時(shí),![]() 沒(méi)有極值點(diǎn),當(dāng)
沒(méi)有極值點(diǎn),當(dāng)![]() 時(shí),
時(shí),![]() 有兩個(gè)極值點(diǎn)
有兩個(gè)極值點(diǎn)![]() ,且
,且![]() .
.
![]() ,
,
∴![]() 又
又![]() ,
,
![]() .記
.記![]() ,
,![]() ,則
,則![]() ,所以
,所以![]() 在
在![]() 時(shí)單調(diào)遞增,
時(shí)單調(diào)遞增,![]() ,所以
,所以![]() ,所以
,所以![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在單調(diào)遞增數(shù)列![]() 中,
中, ![]() ,且
,且![]() 成等差數(shù)列,
成等差數(shù)列,![]() 成等比數(shù)列,
成等比數(shù)列,![]() .
.
(1)①求證:數(shù)列![]() 為等差數(shù)列;
為等差數(shù)列;
②求數(shù)列![]() 通項(xiàng)公式;
通項(xiàng)公式;
(2)設(shè)數(shù)列![]() 的前
的前![]() 項(xiàng)和為
項(xiàng)和為![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示的幾何體![]() 為一簡(jiǎn)單組合體,在底面
為一簡(jiǎn)單組合體,在底面![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)求該組合體![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】“根據(jù)《中華人民共和國(guó)道路交通安全法》規(guī)定:車(chē)輛駕駛員血液酒精濃度在20~80 mg/100ml(不含80)之間,屬于酒后駕車(chē),血液酒精濃度在80mg/100ml(含80)以上時(shí),屬醉酒駕車(chē).”某市交警在該市一交通崗前設(shè)點(diǎn)對(duì)過(guò)往的車(chē)輛進(jìn)行抽查,經(jīng)過(guò)一晚的抽查,共查出酒后駕車(chē)者60名,圖甲是用酒精測(cè)試儀對(duì)這60 名酒后駕車(chē)者血液中酒精濃度進(jìn)行檢測(cè)后依所得結(jié)果畫(huà)出的頻率分布直方圖.
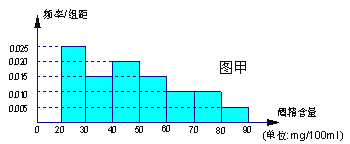
(1)統(tǒng)計(jì)方法中,同一組數(shù)據(jù)常用該組區(qū)間的中點(diǎn)值作為代表,圖乙的程序框圖是對(duì)這60名酒后駕車(chē)者血液的酒精濃度做進(jìn)一步的統(tǒng)計(jì),求出圖乙輸出的S的值,并說(shuō)明S的統(tǒng)計(jì)意義;(圖乙中數(shù)據(jù)![]() 與
與![]() 分別表示圖甲中各組的組中值及頻率)
分別表示圖甲中各組的組中值及頻率)

(2)本次行動(dòng)中,吳、李兩位先生都被酒精測(cè)試儀測(cè)得酒精濃度屬于70~90![]() 的范圍,但他倆堅(jiān)稱(chēng)沒(méi)喝那么多,是測(cè)試儀不準(zhǔn),交警大隊(duì)隊(duì)長(zhǎng)決定在被酒精測(cè)試儀測(cè)得酒精濃度屬于70~90
的范圍,但他倆堅(jiān)稱(chēng)沒(méi)喝那么多,是測(cè)試儀不準(zhǔn),交警大隊(duì)隊(duì)長(zhǎng)決定在被酒精測(cè)試儀測(cè)得酒精濃度屬于70~90![]() 范圍的酒后駕車(chē)者中隨機(jī)抽出2人抽血檢驗(yàn),設(shè)
范圍的酒后駕車(chē)者中隨機(jī)抽出2人抽血檢驗(yàn),設(shè)![]() 為吳、李兩位先生被抽中的人數(shù),求
為吳、李兩位先生被抽中的人數(shù),求![]() 的分布列,并求吳、李兩位先生至少有1人被抽中的概率.
的分布列,并求吳、李兩位先生至少有1人被抽中的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】拋擲兩顆骰子,計(jì)算:
(1)事件“兩顆骰子點(diǎn)數(shù)相同”的概率;
(2)事件“點(diǎn)數(shù)之和小于7”的概率;
(3)事件“點(diǎn)數(shù)之和等于或大于11”的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】函數(shù)![]() 在它的某一個(gè)周期內(nèi)的單調(diào)減區(qū)間是
在它的某一個(gè)周期內(nèi)的單調(diào)減區(qū)間是![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)將![]() 的圖象先向右平移
的圖象先向右平移![]() 個(gè)單位,再將圖象上所有點(diǎn)的橫坐標(biāo)變?yōu)樵瓉?lái)的
個(gè)單位,再將圖象上所有點(diǎn)的橫坐標(biāo)變?yōu)樵瓉?lái)的![]() 倍(縱坐標(biāo)不變),所得到的圖象對(duì)應(yīng)的函數(shù)記為
倍(縱坐標(biāo)不變),所得到的圖象對(duì)應(yīng)的函數(shù)記為![]() ,若對(duì)于任意的
,若對(duì)于任意的![]() ,不等式
,不等式![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知圓![]() 的方程為
的方程為![]() .
.
(I)若點(diǎn)![]() 在圓
在圓![]() 的外部,求
的外部,求![]() 的取值范圍;
的取值范圍;
(II)當(dāng)![]() 時(shí),是否存在斜率為
時(shí),是否存在斜率為![]() 的直線
的直線![]() ,使以
,使以![]() 被圓
被圓![]() 截得的弦
截得的弦![]() 為直徑所作的圓過(guò)原點(diǎn)?若存在,求出
為直徑所作的圓過(guò)原點(diǎn)?若存在,求出![]() 的方程;若不存在,說(shuō)明理由.
的方程;若不存在,說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】宜昌一中江南新校區(qū)擬建一個(gè)扇環(huán)形狀的花壇(如圖所示),按設(shè)計(jì)要求扇環(huán)的周長(zhǎng)為30米,其中大圓弧所在圓的半徑為10米,設(shè)小圓弧所在圓的半徑為![]() 米,圓心角
米,圓心角![]() (弧度).
(弧度).
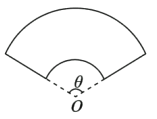
(1)求![]() 關(guān)于
關(guān)于![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(2)已知對(duì)花壇的邊緣(實(shí)線部分)進(jìn)行裝飾時(shí),直線部分的裝飾費(fèi)用為4元/米,弧線部分的裝飾費(fèi)用為9元/米,設(shè)花壇的面積與裝飾總費(fèi)用之比為![]() ,求
,求![]() 關(guān)于
關(guān)于![]() 的函數(shù)關(guān)系式,并求出
的函數(shù)關(guān)系式,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,四棱錐![]() 的底面
的底面![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
, ![]() 是
是![]() 的中點(diǎn),且
的中點(diǎn),且![]() ,
, ![]() .
.

(I)求證: ![]() 平面
平面![]() ;
;
(II)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com