
 如圖所示,五面體ABCDFE中,AB∥CD∥EF,四邊形ABCD,ABEF,CDFE都是等腰梯形,并且平面ABCD⊥平面ABEF,AB=12,CD=3,EF=4,梯形ABCD的高為3,EF到平面ABCD的距離為6,則此五面體的體積為57.
如圖所示,五面體ABCDFE中,AB∥CD∥EF,四邊形ABCD,ABEF,CDFE都是等腰梯形,并且平面ABCD⊥平面ABEF,AB=12,CD=3,EF=4,梯形ABCD的高為3,EF到平面ABCD的距離為6,則此五面體的體積為57. 分析 連結DE、BD,此五面體的體積為V=VD-ABEF+VE-BDC,由此能求出結果.
解答 解:∵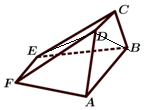 五面體ABCDFE中,AB∥CD∥EF,四邊形ABCD,ABEF,CDFE都是等腰梯形,
五面體ABCDFE中,AB∥CD∥EF,四邊形ABCD,ABEF,CDFE都是等腰梯形,
平面ABCD⊥平面ABEF,AB=12,CD=3,EF=4,梯形ABCD的高為3,EF到平面ABCD的距離為6,
∴S梯形ABEF=$\frac{1}{2}(4+12)×6$=48,
S△BCD=$\frac{1}{2}×3×3$=$\frac{9}{2}$,
連結DE、BD,
∴此五面體的體積為:
V=VD-ABEF+VE-BDC
=$\frac{1}{3}×{S}_{梯形ABEF}×3+\frac{1}{3}×{S}_{△BCD}×3$
=$\frac{1}{3}×48×3+\frac{1}{3}×\frac{9}{2}×6$
=57.
故答案為:57.
點評 本題考查五面體的體積的求法,是中檔題,解題時要認真審題,注意等體積法的合理運用.


 輕松課堂標準練系列答案
輕松課堂標準練系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,9] | B. | (-∞,18] | C. | [9,+∞) | D. | [18,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [-2,-1) | B. | (-∞,-2] | C. | [-2,-1)∪(3,+∞) | D. | (-2,-1)∪(3,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
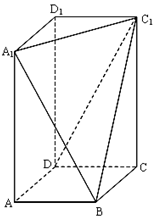 已知長方體ABCD-A1B1C1D1,其中AB=BC=2,過A1、C1、B三點的平面截去長方體的一個角后.得到如圖所示的,且這個幾何體的體積為$\frac{40}{3}$.
已知長方體ABCD-A1B1C1D1,其中AB=BC=2,過A1、C1、B三點的平面截去長方體的一個角后.得到如圖所示的,且這個幾何體的體積為$\frac{40}{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com