
【題目】求所有的正整數![]() 、
、![]() ,使得
,使得![]() 是完全平方數.
是完全平方數.
【答案】見解析
【解析】
由![]()
![]()
![]()
![]()
![]() .
.
設![]() ,
,![]() ).則
).則
![]() .
.
又![]() .
.
設![]() .則
.則
![]() .
.
于是,![]() 是完全平方數.
是完全平方數.
下面證明:不存在互質的正整數![]() ,
,![]() ,使得
,使得![]() 是完全平方數.
是完全平方數.
假設存在,不妨設![]() 是滿足上述要求且使得其和
是滿足上述要求且使得其和![]() 最小的一組正整數.
最小的一組正整數.
因![]()
![]() ,
,
且![]() ,知
,知![]() 、
、![]() 不能同為偶數,所以,
不能同為偶數,所以,![]() 是奇數.
是奇數.
故![]()
![]()
![]() .
.
于是,![]() 與
與![]() 都是完全平方數.
都是完全平方數.
由于![]() 與
與![]() 都是奇數,故可設
都是奇數,故可設
![]() ,
,
![]() .
.
從而,![]() ,且
,且![]() .
.
于是,![]() ,
,![]() 一奇一偶(不妨設
一奇一偶(不妨設![]() 是偶數).
是偶數).
記![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() 、
、![]() 、
、![]() 、
、![]() 為兩兩互質的正整數,且
為兩兩互質的正整數,且![]() 、
、![]() 都是奇數).由對稱性不妨設
都是奇數).由對稱性不妨設![]() .
.
則由![]() ,得
,得
![]()
![]() .
.
又![]() ,
,![]() ,整理得
,整理得
![]()
(1)若![]() 則
則![]()
因為![]() 是奇數,所以,由
是奇數,所以,由![]() ,知
,知![]() 是偶數,
是偶數,![]() 是奇數.
是奇數.
于是,![]() ,矛盾.
,矛盾.
(2)由![]()
![]() .
.
又![]() 是奇數,可設
是奇數,可設
![]() ,
,![]() ,
,![]() .
.
代入![]() ,得
,得![]() .
.
故正整數對![]() 使得
使得![]() 是完全平方數.
是完全平方數.
由于![]() ,這與
,這與![]() 的最小性矛盾.
的最小性矛盾.
(3)由![]()
![]() ,這與
,這與![]() 矛盾.
矛盾.
(4)由![]()
![]() ,
,
這與![]() 矛盾.
矛盾.
綜上,不存在互質的正整數![]() 、
、![]() ,使得
,使得![]() 是完全平方數.
是完全平方數.
故不存在正整數![]() 、
、![]() ,使得
,使得![]() 是完全平方數.
是完全平方數.


科目:高中數學 來源: 題型:
【題目】近年空氣質量逐步惡化,霧霾天氣現象出現增多,大氣污染危害加重.大氣污染可引起心悸、呼吸困難等心肺疾病.為了解某市心肺疾病是否與性別有關,在某醫院隨機對心肺疾病入院的![]() 人進行問卷調查,得到了如下的列聯表:
人進行問卷調查,得到了如下的列聯表:
患心肺疾病 | 不患心肺疾病 | 合計 | |
男 |
|
|
|
女 |
|
|
|
合計 |
|
|
|
(1)用分層抽樣的方法在患心肺疾病的人群中抽![]() 人,其中男性抽多少人?
人,其中男性抽多少人?
(2)在上述抽取的![]() 人中選
人中選![]() 人,求恰好有
人,求恰好有![]() 名女性的概率;
名女性的概率;
(3)為了研究心肺疾病是否與性別有關,請計算出統計量![]() ,你有多大把握認為心肺疾病與性別有關?
,你有多大把握認為心肺疾病與性別有關?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
參考公式:  ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖為我國數學家趙爽(約3世紀初)在為《周髀算經》作注時驗證勾股定理的示意圖,現在提供5種顏色給其中5個小區域涂色,規定每個區域只涂一種顏色,相鄰區域顏色不相同,則不同的涂色方案共有( )
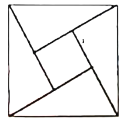
A.360種B.720種C.480種D.420種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是某電視臺主辦的歌手大獎賽上七位評委為甲、乙兩名選手打出的分數的莖葉圖(其中![]() 為數字0~9中的一個),則下列結論中正確的是( )
為數字0~9中的一個),則下列結論中正確的是( )
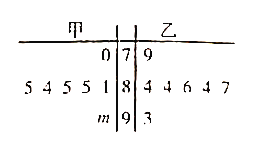
A. 甲選手的平均分有可能和乙選手的平均分相等
B. 甲選手的平均分有可能比乙選手的平均分高
C. 甲選手所有得分的中位數比乙選手所有得分的中位數低
D. 甲選手所有得分的眾數比乙選手所有得分的眾數高
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某醫藥公司研發一種新的保健產品,從一批產品中抽取200盒作為樣本,測量產品的一項質量指標值,該指標值越高越好.由測量結果得到如下頻率分布直方圖:
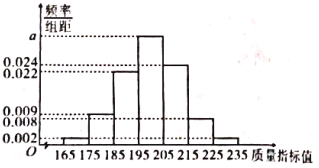
(Ⅰ)求![]() ,并試估計這200盒產品的該項指標的平均值;
,并試估計這200盒產品的該項指標的平均值;
(Ⅱ)① 用樣本估計總體,由頻率分布直方圖認為產品的質量指標值![]() 服從正態分布
服從正態分布![]() ,計算該批產品指標值落在
,計算該批產品指標值落在![]() 上的概率;參考數據:附:若
上的概率;參考數據:附:若![]() ,則
,則![]() ,
,![]() .
.
②國家有關部門規定每盒產品該項指標不低150均為合格,且按指標值的從低到高依次分為:合格、優良、優秀三個等級,其中![]() 為優良,不高于180為合格,不低于220為優秀,在①的條件下,設公司生產該產品1萬盒的成本為15萬元,市場上每盒該產品的等級售價(單位:元)如圖表,求該公司每萬盒的平均利潤.
為優良,不高于180為合格,不低于220為優秀,在①的條件下,設公司生產該產品1萬盒的成本為15萬元,市場上每盒該產品的等級售價(單位:元)如圖表,求該公司每萬盒的平均利潤.
等級 | 合格 | 優良 | 優秀 |
價格 | 10 | 20 | 30 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】計算機考試分理論考試與實際操作兩部分,每部分考試成績只記“合格”與“不合格”,兩部分考試都“合格”者,則計算機考試“合格”,并頒發合格證書甲、乙、丙三人在理論考試中“合格”的概率依次為![]() ,
,![]() ,
,![]() ,在實際操作考試中“合格”的概率依次為
,在實際操作考試中“合格”的概率依次為![]() ,
,![]() ,
,![]() ,所有考試是否合格相互之間沒有影響.
,所有考試是否合格相互之間沒有影響.
(1)假設甲、乙、丙三人同時進行理論與實際操作兩項考試,誰獲得合格證書的可能性最大?
(2)這三人進行理論與實際操作兩項考試后,求恰有兩人獲得合格證書的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】端午節(每年農歷五月初五),是中國傳統節日,有吃粽子的習俗.某超市在端午節這一天,每售出![]() kg粽子獲利潤
kg粽子獲利潤![]() 元,未售出的粽子每
元,未售出的粽子每![]() kg虧損
kg虧損![]() 元.根據歷史資料,得到銷售情況與市場需求量的頻率分布表,如下表所示.該超市為今年的端午節預購進了
元.根據歷史資料,得到銷售情況與市場需求量的頻率分布表,如下表所示.該超市為今年的端午節預購進了![]() kg粽子.以
kg粽子.以![]() (單位:kg,
(單位:kg,![]() )表示今年的市場需求量,
)表示今年的市場需求量,![]() (單位:元)表示今年的利潤.
(單位:元)表示今年的利潤.
市場需求量(kg) |
|
|
|
|
|
頻率 | 0.1 | 0.2 | 0.3 | 0.25 | 0.15 |
(1)將![]() 表示為
表示為![]() 的函數;
的函數;
(2)在頻率分布表的市場需求量分組中,以各組的區間中間值代表該組的各個值,需求量落入該區間的頻率作為需求量取該區間中間值的概率(例如:若需求量![]() ,則取
,則取![]() ,且
,且![]() 的概率等于需求量落入
的概率等于需求量落入![]() 的頻率
的頻率![]() ),求
),求![]() 的數學期望.
的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,已知
中,已知![]() ,
,![]() 為拋物線
為拋物線![]() :
:![]() 上兩點,
上兩點,![]() 為拋物線焦點.分別過
為拋物線焦點.分別過![]() ,
,![]() 作拋物線的切線交于點
作拋物線的切線交于點![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)若![]() ,
,![]() 分別交
分別交![]() 軸于
軸于![]() ,
,![]() 兩點,試問
兩點,試問![]() 的外接圓是否過定點?若是,求出該定點坐標,若不是,請說明理由.
的外接圓是否過定點?若是,求出該定點坐標,若不是,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com