
【題目】已知![]() 個正整數,它們的平均數是
個正整數,它們的平均數是![]() ,中位數是
,中位數是![]() ,唯一眾數是
,唯一眾數是![]() ,則這
,則這![]() 個數方差的最大值為__________.(精確到小數點后一位)
個數方差的最大值為__________.(精確到小數點后一位)
 期末集結號系列答案
期末集結號系列答案科目:高中數學 來源: 題型:
【題目】2018年6月14日,世界杯足球賽在俄羅斯拉開帷幕,世界杯給俄羅斯經濟帶來了一定的增長,某紀念商品店的銷售人員為了統計世界杯足球賽期間商品的銷售情況,隨機抽查了該商品商店某天200名顧客的消費金額情況,得到如圖頻率分布表:將消費顧客超過4萬盧布的顧客定義為”足球迷”,消費金額不超過4萬盧布的顧客定義為“非足球迷”。
消費金額/萬盧布 |
|
|
|
|
|
| 合計 |
顧客人數 | 9 | 31 | 36 | 44 | 62 | 18 | 200 |
(1)求這200名顧客消費金額的中位數與平均數(同一組中的消費金額用該組的中點值作代表;
(2)該紀念品商店的銷售人員為了進一步了解這200名顧客喜歡紀念品的類型,采用分層抽樣的方法從“非足球迷”,“足球迷”中選取5人,再從這5人中隨機選取3人進行問卷調查,則選取的3人中“非足球迷”人數的分布列和數學期望。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某部門在同一上班高峰時段對甲、乙兩座地鐵站各隨機抽取了50名乘客,統計其乘車等待時間(指乘客從進站口到乘上車的時間,乘車等待時間不超過40分鐘).將統計數據按![]() ,
,![]() ,
,![]() ,
,![]() 分組,制成頻率分布直方圖:
分組,制成頻率分布直方圖:

(1)求![]() 的值;
的值;
(2)記![]() 表示事件“在上班高峰時段某乘客在甲站乘車等待時間少于20分鐘”,試估計
表示事件“在上班高峰時段某乘客在甲站乘車等待時間少于20分鐘”,試估計![]() 的概率;
的概率;
(3)假設同組中的每個數據用該組區間左端點值來估計,記在上班高峰時段甲、乙兩站各抽取的50名乘客乘車的平均等待時間分別為![]() ,
,![]() ,求
,求![]() 的值,并直接寫出
的值,并直接寫出![]() 與
與![]() 的大小關系.
的大小關系.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在長方體![]() 中,
中,![]() 點
點![]() 是棱
是棱![]() 的中點,點
的中點,點![]() 在棱
在棱![]() 上,且
上,且![]() (
(![]() 為實數).
為實數).

(1)求二面角![]() 的余弦值;
的余弦值;
(2)當![]() 時,求直線
時,求直線![]() 與平面
與平面![]() 所成角的正弦值的大小;
所成角的正弦值的大小;
(3)求證:直線![]() 與直線
與直線![]() 不可能垂直.
不可能垂直.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】浦東一模之后的“大將” 洗心革面,再也沒進過網吧,開始發奮學習. 2019年春節檔非常熱門的電影《流浪地球》引發了他的思考:假定地球(設為質點![]() ,地球半徑忽略不計)借助原子發動機開始流浪的軌道是以木星(看作球體,其半徑約為
,地球半徑忽略不計)借助原子發動機開始流浪的軌道是以木星(看作球體,其半徑約為![]() 萬米)的中心
萬米)的中心![]() 為右焦點的橢圓
為右焦點的橢圓![]() . 已知地球的近木星點
. 已知地球的近木星點![]() (軌道上離木星表面最近的點)到木星表面的距離為
(軌道上離木星表面最近的點)到木星表面的距離為![]() 萬米,遠木星點
萬米,遠木星點![]() (軌道上離木星表面最遠的點)到木星表面的距離為
(軌道上離木星表面最遠的點)到木星表面的距離為![]() 萬米.
萬米.

(1)求如圖給定的坐標系下橢圓![]() 的標準方程;
的標準方程;
(2)若地球在流浪的過程中,由![]() 第一次逆時針流浪到與軌道中心
第一次逆時針流浪到與軌道中心![]() 的距離為
的距離為![]() 萬米時(其中
萬米時(其中![]() 分別為橢圓的長半軸、短半軸的長),由于木星引力,部分原子發動機突然失去了動力,此時地球向著木星方向開始變軌(如圖所示),假定地球變軌后的軌道為一條直線
分別為橢圓的長半軸、短半軸的長),由于木星引力,部分原子發動機突然失去了動力,此時地球向著木星方向開始變軌(如圖所示),假定地球變軌后的軌道為一條直線![]() ,稱該直線的斜率
,稱該直線的斜率![]() 為“變軌系數”. 求“變軌系數”
為“變軌系數”. 求“變軌系數”![]() 的取值范圍,使地球與木星不會發生碰撞. (精確到小數點后一位)
的取值范圍,使地球與木星不會發生碰撞. (精確到小數點后一位)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為了解某產品的獲利情況,將今年1至7月份的銷售收入![]() (單位:萬元)與純利潤
(單位:萬元)與純利潤![]() (單位:萬元)的數據進行整理后,得到如下表格:
(單位:萬元)的數據進行整理后,得到如下表格:
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
銷售收入 | 13 | 13.5 | 13.8 | 14 | 14.2 | 14.5 | 15 |
純利潤 | 3.2 | 3.8 | 4 | 4.2 | 4.5 | 5 | 5.5 |
該公司先從這7組數據中選取5組數據求純利潤![]() 關于銷售收入
關于銷售收入![]() 的線性回歸方程,再用剩下的2組數據進行檢驗.假設選取的是2月至6月的數據.
的線性回歸方程,再用剩下的2組數據進行檢驗.假設選取的是2月至6月的數據.
(1)求純利潤![]() 關于銷售收入
關于銷售收入的線性回歸方程(精確到0.01);
(2)若由線性回歸方程得到的估計數據與檢驗數據的誤差均不超過0.1萬元,則認為得到的線性回歸方程是理想的.試問該公司所得線性回歸方程是否理想?
參考公式:![]() ,
, ,
,![]() ,
,![]() ;參考數據:
;參考數據:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】國家統計局統計了我國近10年(2009年2018年)的GDP(GDP是國民經濟核算的核心指標,也是衡量一個國家或地區總體經濟狀況的重要指標)增速的情況,并繪制了下面的折線統計圖.
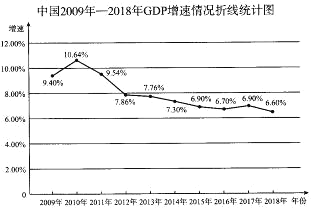
根據該折線統計圖,下面說法錯誤的是
A. 這10年中有3年的GDP增速在9.00%以上
B. 從2010年開始GDP的增速逐年下滑
C. 這10年GDP仍保持6.5%以上的中高速增長
D. 2013年—2018年GDP的增速相對于2009年—2012年,波動性較小
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別為線段
分別為線段![]() ,
,![]() 上的點,且
上的點,且![]() ,
,![]() ,
,![]() .
.
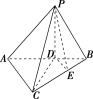
(1)求證:![]() 平面
平面![]() ;
;
(2)若直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,求平面
,求平面![]() 與平面
與平面![]() 所成的銳二面角.
所成的銳二面角.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com