
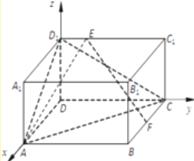
【題目】如圖,在長方體![]() 中,
中,![]() 點
點![]() 是棱
是棱![]() 的中點,點
的中點,點![]() 在棱
在棱![]() 上,且
上,且![]() (
(![]() 為實數).
為實數).

(1)求二面角![]() 的余弦值;
的余弦值;
(2)當![]() 時,求直線
時,求直線![]() 與平面
與平面![]() 所成角的正弦值的大小;
所成角的正弦值的大小;
(3)求證:直線![]() 與直線
與直線![]() 不可能垂直.
不可能垂直.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)見解析.
;(3)見解析.
【解析】分析:(1)建立如圖所示的空間直角坐標系,寫出相應點的坐標,算出相應向量的坐標,利用垂直向量的數量積等于零的方法建立方程組,算出平面對應的法向量,之后應用平面的法向量所成角的余弦值求得二面角的余弦值;’
(2)當![]() 時,可得E,F的坐標,從而求得
時,可得E,F的坐標,從而求得![]() 的坐標,進而算出
的坐標,進而算出![]() 的余弦值,再由其為銳角,結合直線與平面所成角的定義,即可算出直線與平面所成角的正弦值的大小;
的余弦值,再由其為銳角,結合直線與平面所成角的定義,即可算出直線與平面所成角的正弦值的大小;
(3)假設直線![]() 與直線
與直線![]() 垂直,根據向量的數量積等于零,建立關于
垂直,根據向量的數量積等于零,建立關于![]() 的等量關系式,化簡可得
的等量關系式,化簡可得![]() ,由根的判別式小于零得該方程無解,從而得到假設不成立,從而得到原結論成立.
,由根的判別式小于零得該方程無解,從而得到假設不成立,從而得到原結論成立.
詳解:(1)如圖所示,建立空間直角坐標系![]() .
.
則![]()
![]()
![]() ,
,![]()
設平面![]() 的法向量為
的法向量為![]() ,
,
則![]() .即
.即![]() .令
.令![]() ,則
,則![]() .
.
∴平面![]() 的一個法向量
的一個法向量![]() .又平面
.又平面![]() 的一個法向量為
的一個法向量為![]() .
.
故![]() ,即二面角
,即二面角![]() 的余弦值為
的余弦值為![]() .
.
(2)當λ =![]() 時,E(0,1,2),F(1,4,0),
時,E(0,1,2),F(1,4,0),![]() .
.
所以![]() .
.
因為 ![]() ,所以
,所以![]() 為銳角,
為銳角,
從而直線EF與平面![]() 所成角的正弦值的大小為
所成角的正弦值的大小為![]() .
.
(3)假設![]() ,則
,則![]() .
.
∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .化簡得
.化簡得![]() .
.
該方程無解,所以假設不成立,即直線![]() 不可能與直線
不可能與直線![]() 不可能垂直.
不可能垂直.


 字詞句篇與同步作文達標系列答案
字詞句篇與同步作文達標系列答案 走進文言文系列答案
走進文言文系列答案科目:高中數學 來源: 題型:
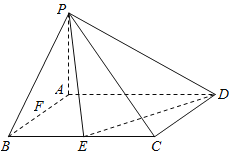
【題目】在四棱錐![]() 中,底面ABCD是矩形,
中,底面ABCD是矩形,![]() 平面ABCD,
平面ABCD,![]() ,E,F是線段BC,AB的中點.
,E,F是線段BC,AB的中點.
![]() Ⅰ
Ⅰ![]() 證明:
證明:![]() ;
;
![]() Ⅱ
Ⅱ![]() 在線段PA上確定點G,使得
在線段PA上確定點G,使得![]() 平面PED,請說明理由.
平面PED,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班級共派出![]() 個男生和
個男生和![]() 個女生參加學校運動會的入場儀式,其中男生倪某為領隊.入場時,領隊男生倪某必須排第一個,然后女生整體在男生的前面,排成一路縱隊入場,共有
個女生參加學校運動會的入場儀式,其中男生倪某為領隊.入場時,領隊男生倪某必須排第一個,然后女生整體在男生的前面,排成一路縱隊入場,共有![]() 種排法;入場后,又需從男生(含男生倪某)和女生中各選一名代表到主席臺服務,共有
種排法;入場后,又需從男生(含男生倪某)和女生中各選一名代表到主席臺服務,共有![]() 種選法.(1)試求
種選法.(1)試求![]() 和
和![]() ; (2)判斷
; (2)判斷![]() 和
和![]() 的大小(
的大小(![]() ),并用數學歸納法證明.
),并用數學歸納法證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() +
+ ![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為 ![]() ,與雙曲線x2﹣y2=1的漸近線有四個交點,以這四個交點為頂點的四邊形的面積為16,則橢圓C的方程為( )
,與雙曲線x2﹣y2=1的漸近線有四個交點,以這四個交點為頂點的四邊形的面積為16,則橢圓C的方程為( )
A.![]() +
+ ![]() =1
=1
B.![]() +
+ ![]() =1
=1
C.![]() +
+ ![]() =1
=1
D.![]() +
+ ![]() =1
=1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列{an}的前n項和記為Sn , a1=t,an+1=2Sn+1(n∈N*).
(1)當t為何值時,數列{an}為等比數列?
(2)在(1)的條件下,若等差數列{bn}的前n項和Tn有最大值,且T3=15,又a1+b1 , a2+b2 , a3+b3成等比數列,求Tn .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com