
分析 求出P的軌跡方程,由動點P在直線x+$\sqrt{3}$y+b=0上,滿足PB=2PA的點P有且只有兩個,
轉(zhuǎn)化為直線與圓x2+y2+$\frac{8}{3}$x-$\frac{16}{3}$=0相交,即可求出實數(shù)b的取值范圍.
解答 解:由題意O(0,0),O1(4,0),設P(x,y),則
∵PB=2PA,
∴(x-4)2+y2=4(x2+y2),
∴x2+y2+$\frac{8}{3}$x-$\frac{16}{3}$=0,
其圓心坐標為(-$\frac{4}{3}$,0),半徑為$\frac{8}{3}$;
∵動點P在直線x+$\sqrt{3}$y+b=0上,滿足PB=2PA的點P有且只有兩個,
∴該直線與圓x2+y2+$\frac{8}{3}$x-$\frac{16}{3}$=0相交,
∴圓心到直線的距離滿足d=$\frac{|-\frac{4}{3}+0+b|}{\sqrt{{1}^{2}{+(\sqrt{3})}^{2}}}$<$\frac{8}{3}$,
化簡得|b-$\frac{4}{3}$|<$\frac{16}{3}$,
解得-4<b<$\frac{20}{3}$,
∴實數(shù)b的取值范圍是(-4,$\frac{20}{3}$).
故答案為:(-4,$\frac{20}{3}$).
點評 本題考查求點的軌跡方程以及直線與圓的位置關(guān)系的應用問題,正確轉(zhuǎn)化是解題的關(guān)鍵,是綜合性題目.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | an=2n | B. | an=2n-1 | C. | an=2n-1 | D. | an=2n-1-1 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | $\frac{2a}{b}$ | B. | 2a-b | C. | a2-b | D. | $\frac{a^2}{b}$ |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
| 零件的個數(shù)x(個) | 2 | 3 | 4 | 5 |
| 加工的時間y(小時) | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
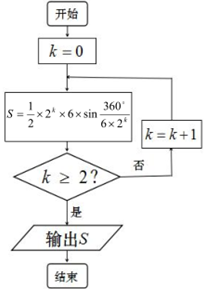 公元263年左右,我國數(shù)學家劉徽發(fā)現(xiàn)當圓內(nèi)接正多邊形的邊數(shù)無限增加時,多邊形面積可無限逼近于圓的面積,并創(chuàng)立了“割圓術(shù)”,利用“割圓術(shù)”劉徽得到了圓周率精確到小數(shù)點后兩位的近似值3.14,這就是著名的“徽率”.如圖是利用劉徽的“割圓術(shù)”思想設計的一個程序框圖,則輸出的(四舍五入精確到小數(shù)點后兩位)的值為( )(參考數(shù)據(jù):sin15°=0.2588,sin75°=0.1305)
公元263年左右,我國數(shù)學家劉徽發(fā)現(xiàn)當圓內(nèi)接正多邊形的邊數(shù)無限增加時,多邊形面積可無限逼近于圓的面積,并創(chuàng)立了“割圓術(shù)”,利用“割圓術(shù)”劉徽得到了圓周率精確到小數(shù)點后兩位的近似值3.14,這就是著名的“徽率”.如圖是利用劉徽的“割圓術(shù)”思想設計的一個程序框圖,則輸出的(四舍五入精確到小數(shù)點后兩位)的值為( )(參考數(shù)據(jù):sin15°=0.2588,sin75°=0.1305)| A. | 3.10 | B. | 3.11 | C. | 3.12 | D. | 3.13 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com