
【題目】《基礎教育課程改革綱要(試行)》將“具有良好的心理素質”列入新課程的培養目標.為加強心理健康教育工作的開展,不斷提高學生的心理素質,九江市某校高二年級開設了《心理健康》選修課,學分為2分.學校根據學生平時上課表現給出“合格”與“不合格”兩種評價,獲得“合格”評價的學生給予50分的平時分,獲得“不合格”評價的學生給予30分的平時分,另外還將進行一次測驗.學生將以“平時分×40%+測驗分×80%”作為“最終得分”,“最終得分”不少于60分者獲得學分.
該校高二(1)班選修《心理健康》課的學生的平時分及測驗分結果如下:
測驗分 | [30,40) | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
平時分50分人數 | 0 | 1 | 1 | 3 | 4 | 4 | 2 |
平時分30分人數 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
(1)根據表中數據完成如下2×2列聯表,并分析是否有95%的把握認為這些學生“測驗分是否達到60分”與“平時分”有關聯?
選修人數 | 測驗分 達到60分 | 測驗分 未達到60分 | 合計 |
平時分50分 | |||
平時分30分 | |||
合計 |
(2)用樣本估計總體,若從所有選修《心理健康》課的學生中隨機抽取5人,設獲得學分人數為![]() ,求
,求![]() 的期望.
的期望.
附:![]() ,其中
,其中![]()
| 0.1 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879/p> | 10.828 |
【答案】(1)有95%的把握認為學生“測驗分是否達到60分”與“平時分”有關聯;(2)4
【解析】
(1)根據數據填表,然后計算![]() ,可得結果.
,可得結果.
(2)根據計算,可得未獲得分數的人數,然后可知獲得分數的概率,依據二項分布數學期望的計算方法,可得結果.
解:(1)根據表中數據統計,可得2x2列聯表
選修人數 | 測驗分 | 合計 | |
達到60分 | 未達到60分 | ||
平時分50分 | 13 | 2 | 15 |
平時分30分 | 2 | 3 | 5 |
合計 | 15 | 5 | 20 |
![]()
![]() ,
,
∴有95%的把握認為學生“測驗分是否達到60分”與“平時分”有關聯
(2)分析學生得分,![]() ,
,
![]() ,
,
平時分50分的學生中測驗分只需達到50分,
而平時分30分的學生中測驗分必須達到60分,才能獲得學分
平時分50分的學生測驗分未達到50分的只有1人,
平時分30分的學生測驗分未達到60分的有3人
∴從這些學生中隨機抽取1人,
該生獲得學分的概率為![]()
![]() ,
,![]() .
.


 習題精選系列答案
習題精選系列答案科目:高中數學 來源: 題型:
【題目】中國“一帶一路”戰略構思提出后, 某科技企業為抓住“一帶一路”帶來的機遇, 決定開發生產一款大型電子設備, 生產這種設備的年固定成本為![]() 萬元, 每生產
萬元, 每生產![]() 臺,需另投入成本
臺,需另投入成本![]() (萬元), 當年產量不足
(萬元), 當年產量不足![]() 臺時,
臺時,![]() (萬元); 當年產量不小于
(萬元); 當年產量不小于![]() 臺時
臺時![]() (萬元), 若每臺設備售價為
(萬元), 若每臺設備售價為![]() 萬元, 通過市場分析,該企業生產的電子設備能全部售完.
萬元, 通過市場分析,該企業生產的電子設備能全部售完.
(1)求年利潤![]() (萬元)關于年產量
(萬元)關于年產量![]() (臺)的函數關系式;
(臺)的函數關系式;
(2)年產量為多少臺時 ,該企業在這一電子設備的生產中所獲利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】點P為兩直線l1:3x+4y﹣2=0和l2:2x+y+2=0的交點.
(1)求過P點且與直線3x﹣2y+4=0平行的直線方程;
(2)求過原點且與直線l1和l2圍成的三角形為直角三角形的直線方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() :
:![]() (
(![]() )上橫坐標為4的點到焦點的距離為5.
)上橫坐標為4的點到焦點的距離為5.
(1)求拋物線![]() 的方程;
的方程;
(2)設直線![]() 與拋物線
與拋物線![]() 交于不同兩點
交于不同兩點![]() ,若滿足
,若滿足![]() ,證明直線
,證明直線![]() 恒過定點,并求出定點
恒過定點,并求出定點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,橢圓
中,橢圓![]() 的參數方程為
的參數方程為![]() 為參數).以坐標原點
為參數).以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,直線
軸的正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為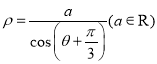 ,直線
,直線![]() 經過橢圓
經過橢圓![]() 的右焦點
的右焦點![]() .
.
(1)求實數![]() 的值;
的值;
(2)設直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知橢圓C:![]() 的短軸長為2,傾斜角為
的短軸長為2,傾斜角為![]() 的直線l與橢圓C相交于A,B兩點,線段AB的中點為M,且點M與坐標原點O連線的斜率為
的直線l與橢圓C相交于A,B兩點,線段AB的中點為M,且點M與坐標原點O連線的斜率為![]() .
.
(1)求橢圓C的標準方程;
(2)若![]() ,P是以AB為直徑的圓上的任意一點,求證:
,P是以AB為直徑的圓上的任意一點,求證:![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com