
(本小題10分)已知圓C:x2+(y-3)2=4,一動直線l過A(-1,0)與圓C相交于P,Q兩點,M是PQ的中點,l與直線m:x+3y+6=0相交于點N.
(Ⅰ)求證:當(dāng)l與m垂直時,l經(jīng)過圓心C;
(Ⅱ)當(dāng)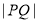 =2
=2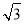 時,求直線l的方程;
時,求直線l的方程;
(Ⅲ)請問: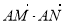 是否與直線l的傾斜角有關(guān),若無關(guān),請求出其值;若有關(guān),請說明理由.
是否與直線l的傾斜角有關(guān),若無關(guān),請求出其值;若有關(guān),請說明理由.
(Ⅰ)(Ⅱ)(Ⅲ)見解析
【解析】
試題分析:(Ⅰ)根據(jù)已知求出直線方程后再驗證圓心滿足所求直線方程;(Ⅱ)設(shè)圓的半徑為r,弦心距為d,弦長為l,則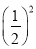 =r2-d2.利用此公式即可求得直線方程,注意斜率的討論;(Ⅲ)有關(guān)探索性問題,一般是先假設(shè)存在滿足題意的元素,經(jīng)過推理論證,如果得到可以成立的結(jié)果,就可作出存在的結(jié)論;若得到與已知條件、定義、公理、定理、性質(zhì)相矛盾的結(jié)果,則說明假設(shè)不存在.
=r2-d2.利用此公式即可求得直線方程,注意斜率的討論;(Ⅲ)有關(guān)探索性問題,一般是先假設(shè)存在滿足題意的元素,經(jīng)過推理論證,如果得到可以成立的結(jié)果,就可作出存在的結(jié)論;若得到與已知條件、定義、公理、定理、性質(zhì)相矛盾的結(jié)果,則說明假設(shè)不存在.
試題解析:(1)∵直線l與直線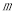 垂直,且
垂直,且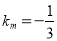
∴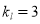 ,又
,又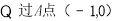
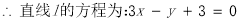
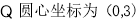
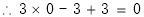 ,即圓心在直線上.
,即圓心在直線上.
 當(dāng)直線l與m垂直時,直線l必過圓心C. 3分
當(dāng)直線l與m垂直時,直線l必過圓心C. 3分
(2)①當(dāng)直線l與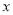 軸垂直時,易知
軸垂直時,易知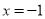 符合題意. 4分
符合題意. 4分
②當(dāng)直線l與 軸不垂直時,設(shè)直線l的方程為
軸不垂直時,設(shè)直線l的方程為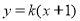 ,即
,即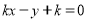 .
.
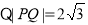 ,
,
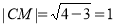 .
.
則由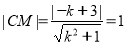 ,得
,得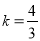 .
.
∴直線l: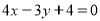 .
.
從而所求直線l的方程為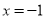 或
或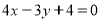 6分
6分
(3)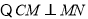 ,
,
∴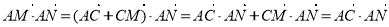

①當(dāng)直線l與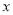 軸垂直,易得
軸垂直,易得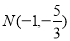 ,則
,則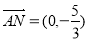
又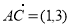 ,
,
∴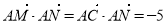 7分
7分
②當(dāng)l的斜率存在時,設(shè)直線l的方程為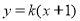 ,
,
則由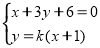 ,得
,得 . 8分
. 8分
則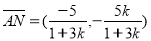 .
.
∴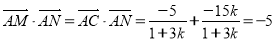 . 9分
. 9分
綜上,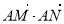 與直線l的斜率無關(guān),且
與直線l的斜率無關(guān),且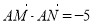 . 10分
. 10分
考點:解析幾何的綜合應(yīng)用


科目:高中數(shù)學(xué) 來源:2014-2015學(xué)年重慶市高二上學(xué)期期中考試?yán)砜茢?shù)學(xué)試卷(解析版) 題型:填空題
過點P(3,1)向圓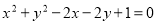 作一條切線,切點為A,則切線段PA的長為 .
作一條切線,切點為A,則切線段PA的長為 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014-2015學(xué)年廣東省高二上學(xué)期期中考試文科數(shù)學(xué)試卷(解析版) 題型:填空題
在等比數(shù)列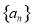 中,已知
中,已知 ,則公比q =_____
,則公比q =_____
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014-2015學(xué)年北京市高二上學(xué)期期中練習(xí)文科數(shù)學(xué)試卷(解析版) 題型:填空題
已知平面 ,
,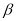 和直線
和直線  ,則滿足下列條件中_______(填上所有正確的序號)
,則滿足下列條件中_______(填上所有正確的序號)
能使 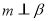 成立.
成立.
① ,②
,② ;③
;③ ;④
;④ .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014-2015學(xué)年北京市高二上學(xué)期期中練習(xí)文科數(shù)學(xué)試卷(解析版) 題型:選擇題
某幾何體的三視圖如圖所示,則該幾何體的體積是( )
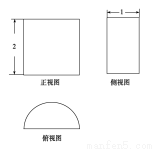
A.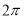 B.
B.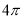 C.
C.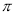 D.
D.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014-2015學(xué)年北京市高二上學(xué)期期中練習(xí)理科數(shù)學(xué)試卷(解析版) 題型:填空題
已知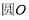 :
: ,點
,點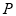 是
是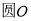 上的一動點,則
上的一動點,則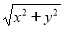 的最大值是________;
的最大值是________; 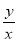 的最小值是_______.
的最小值是_______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014-2015學(xué)年北京市高二上學(xué)期期中練習(xí)理科數(shù)學(xué)試卷(解析版) 題型:選擇題
直線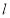 與兩直線
與兩直線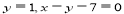 分別交于
分別交于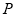 ,
,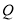 兩點,線段
兩點,線段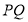 的中點是
的中點是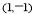 則
則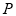 點的坐標(biāo)為( )
點的坐標(biāo)為( )
A.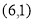 B.
B.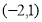 C.
C. 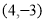 D.
D.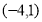
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014-2015學(xué)年內(nèi)蒙古一機一中高一上學(xué)期期中考試數(shù)學(xué)試卷(解析版) 題型:選擇題
出租車按如下方法收費:起步價7元,可行3 (不含3
(不含3 );3
);3 到7
到7 (不含7
(不含7 )按
)按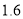 元/
元/ 計價(不足1
計價(不足1 按1
按1 計算);7
計算);7 以后按
以后按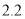 元/
元/ 計價,到目的地結(jié)算時還需付1元的燃油附加費.若從甲地坐出租車到乙地(路程
計價,到目的地結(jié)算時還需付1元的燃油附加費.若從甲地坐出租車到乙地(路程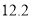
 ),需付車費(精確到1元) ( )
),需付車費(精確到1元) ( )
A、28元 B、27元 C、26元 D、25元
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014-2015學(xué)年湖北省高二上學(xué)期期中考試文科數(shù)學(xué)試卷(解析版) 題型:填空題
若數(shù)據(jù)組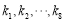 的平均數(shù)為4,方差為2,則
的平均數(shù)為4,方差為2,則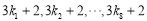 的平均數(shù)為
的平均數(shù)為 ,方差為
,方差為 .
.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com