
【題目】在平行四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是EA的中點(如圖1),將
是EA的中點(如圖1),將![]() 沿CD折起到圖2中
沿CD折起到圖2中![]() 的位置,得到四棱錐是
的位置,得到四棱錐是![]() .
.
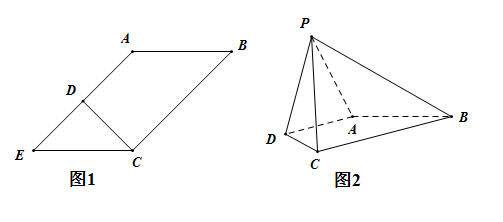
(1)求證:![]() 平面PDA;
平面PDA;
(2)若PD與平面ABCD所成的角為![]() .且
.且![]() 為銳角三角形,求平面PAD和平面PBC所成銳二面角的余弦值.
為銳角三角形,求平面PAD和平面PBC所成銳二面角的余弦值.
【答案】(1)證明見解析; (2)![]()
【解析】
(1)證明![]() ,
,![]() ,即可證明線面垂直;
,即可證明線面垂直;
(2)由線面角求得![]() ,以
,以![]() 中點
中點![]() 為坐標原點建立直角坐標系,由向量法求得二面角的余弦值.
為坐標原點建立直角坐標系,由向量法求得二面角的余弦值.
(1)將![]() 沿CD折起過程中,
沿CD折起過程中,![]() 平面PDA成立.證明如下:
平面PDA成立.證明如下:
![]() 是EA的中點,
是EA的中點,![]() ,
,![]() ,
,
在![]() 中,由余弦定理得,
中,由余弦定理得,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 為等腰直角三角形且
為等腰直角三角形且![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() 平面PDA.
平面PDA.
(2)由(1)知![]() 平面PDA,
平面PDA,![]() 平面ABCD,
平面ABCD,
![]() 平面
平面![]() 平面ABCD,
平面ABCD,
![]() 為銳角三角形,
為銳角三角形,
![]() 在平面ABCD內的射影必在棱AD上,記為O,連接PO,
在平面ABCD內的射影必在棱AD上,記為O,連接PO,![]() 平面ABCD,
平面ABCD,
則![]() 是PD與平面ABCD所成的角,
是PD與平面ABCD所成的角,
![]() ,
,
![]() ,
,
![]() 為等邊三角形,O為AD的中點,
為等邊三角形,O為AD的中點,
故以O為坐標原點,過點O且與CD平行的直線為x軸,
DA所在直線為y軸,OP所在直線為z軸建立如圖所示的空間直角坐標系,
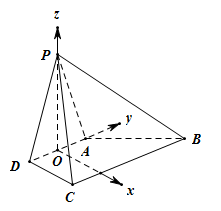
設x軸與BC交于點M,
![]() ,
,![]()
易知![]()
![]() ,
,
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() 平面PDA,
平面PDA,
![]() 可取平面PDA的一個法向量
可取平面PDA的一個法向量![]() ,
,
設平面PBC的法向量![]() ,
,
則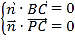 ,即
,即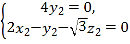 ,
,
令![]() ,則
,則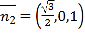 為平面PBC的一個法向量,
為平面PBC的一個法向量,
設平面PAD和平面PBC所成的角為![]() ,
,
由圖易知![]() 為銳角,
為銳角,
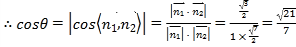 .
.
![]() 平面PAD和平面PBC所成角的余弦值為
平面PAD和平面PBC所成角的余弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】若拋物線![]() 的焦點為
的焦點為![]() ,
,![]() 是坐標原點,
是坐標原點,![]() 為拋物線上的一點,向量
為拋物線上的一點,向量![]() 與
與![]() 軸正方向的夾角為60°,且
軸正方向的夾角為60°,且![]() 的面積為
的面積為![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)若拋物線![]() 的準線與
的準線與![]() 軸交于點
軸交于點![]() ,點
,點![]() 在拋物線
在拋物線![]() 上,求當
上,求當![]() 取得最大值時,直線
取得最大值時,直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著食品安全問題逐漸引起人們的重視,有機、健康的高端綠色蔬菜越來越受到消費者的歡迎,同時生產—運輸—銷售一體化的直銷供應模式,不僅減少了成本,而且減去了蔬菜的二次污染等問題.
(1)在有機蔬菜的種植過程中,有機肥料使用是必不可少的.根據統計某種有機蔬菜的產量與有機肥料的用量有關系,每個有機蔬菜大棚產量的增加量![]() (百斤)與使用堆漚肥料
(百斤)與使用堆漚肥料![]() (千克)之間對應數據如下表
(千克)之間對應數據如下表
使用堆漚肥料 | 2 | 4 | 5 | 6 | 8 |
產量的增加量 | 3 | 4 | 4 | 4 | 5 |
依據表中的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;并根據所求線性回歸方程,估計如果每個有機蔬菜大棚使用堆漚肥料10千克,則每個有機蔬菜大棚產量增加量
;并根據所求線性回歸方程,估計如果每個有機蔬菜大棚使用堆漚肥料10千克,則每個有機蔬菜大棚產量增加量![]() 是多少百斤?
是多少百斤?
(2)某大棚蔬菜種植基地將采摘的有機蔬菜以每份三斤稱重并保鮮分裝,以每份10元的價格銷售到生鮮超市.“樂購”生鮮超市以每份15元的價格賣給顧客,如果當天前8小時賣不完,則超市通過促銷以每份5元的價格賣給顧客(根據經驗,當天能夠把剩余的有機蔬菜都低價處理完畢,且處理完畢后,當天不再進貨).該生鮮超市統計了100天有機蔬菜在每天的前8小時內的銷售量(單位:份),制成如下表格(注:![]() ,且
,且![]() );
);
前8小時內的銷售量(單位:份) | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
頻數 | 10 | x | 16 | 6 | 15 | 13 | y |
若以100天記錄的頻率作為每日前8小時銷售量發生的概率,該生鮮超市當天銷售有機蔬菜利潤的期望值為決策依據,當購進17份比購進18份的利潤的期望值大時,求![]() 的取值范圍.
的取值范圍.
附:回歸直線方程為![]() ,其中
,其中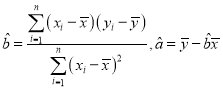 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為進一步規范校園管理,強化飲食安全,提出了“遠離外賣,健康飲食”的口號.當然,也需要學校食堂能提供安全豐富的菜品來滿足同學們的需求.在學期末,校學生會為了調研學生對本校食堂A部和B部的用餐滿意度,從在A部和B部都用過餐的學生中隨機抽取了200人,每人分別對其評分,滿分為100分.隨后整理評分數據,將分數分成6組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4組
,第4組![]() ,第5組
,第5組![]() ,第6組
,第6組![]() ,得到A部分數的頻率分布直方圖和B部分數的頻數分布表.
,得到A部分數的頻率分布直方圖和B部分數的頻數分布表.
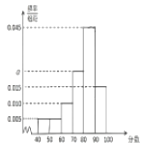
分數區間 | 頻數 |
| 7 |
| 18 |
| 21 |
| 24 |
| 70 |
| 60 |
定義:學生對食堂的“滿意度指數”
分數 |
|
|
|
|
|
|
滿意度指數 | 0 | 1 | 2 | 3 | 4 | 5 |
(1)求A部得分的中位數(精確到小數點后一位);
(2)A部為進一步改善經營,從打分在80分以下的前四組中,采用分層抽樣的方法抽取8人進行座談,再從這8人中隨機抽取3人參與“端午節包粽子”實踐活動,在第3組抽到1人的情況下,第4組抽到2人的概率;
(3)如果根據調研結果評選學生放心餐廳,應該評選A部還是B部(將頻率視為概率)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C1:x2=2py(p>0),圓C2:x2+y2﹣8y+12=0的圓心M到拋物線C1的準線的距離為![]() ,點P是拋物線C1上一點,過點P,M的直線交拋物線C1于另一點Q,且|PM|=2|MQ|,過點P作圓C2的兩條切線,切點為A、B.
,點P是拋物線C1上一點,過點P,M的直線交拋物線C1于另一點Q,且|PM|=2|MQ|,過點P作圓C2的兩條切線,切點為A、B.
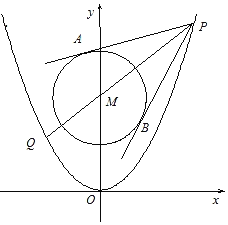
(Ⅰ)求拋物線C1的方程;
(Ⅱ)求直線PQ的方程及![]()
![]()
![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了更好地支持“中小型企業”的發展,某市決定對部分企業的稅收進行適當的減免,某機構調查了當地的中小型企業年收入情況,并根據所得數據畫出了樣本的頻率分布直方圖,下面三個結論:
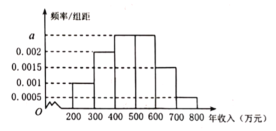
①樣本數據落在區間![]() 的頻率為0.45;
的頻率為0.45;
②如果規定年收入在500萬元以內的企業才能享受減免稅政策,估計有55%的當地中小型企業能享受到減免稅政策;
③樣本的中位數為480萬元.
其中正確結論的個數為( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
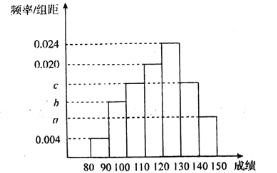
【題目】高三年級某班50名學生期中考試數學成績的頻率分布直方圖如圖所示,成績分組區間為:![]()
![]()
![]()
![]()
![]()
![]()
![]() .其中a,b,c成等差數列且
.其中a,b,c成等差數列且![]() .物理成績統計如表.(說明:數學滿分150分,物理滿分100分)
.物理成績統計如表.(說明:數學滿分150分,物理滿分100分)
分組 |
|
|
|
|
|
頻數 | 6 | 9 | 20 | 10 | 5 |
(1)根據頻率分布直方圖,請估計數學成績的平均分;
(2)根據物理成績統計表,請估計物理成績的中位數;
(3)若數學成績不低于140分的為“優”,物理成績不低于90分的為“優”,已知本班中至少有一個“優”同學總數為6人,從此6人中隨機抽取3人,記X為抽到兩個“優”的學生人數,求X的分布列和期望值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com