
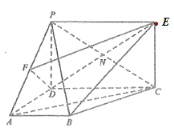
【題目】如圖所示的幾何體中,![]() 垂直于梯形
垂直于梯形![]() 所在的平面,
所在的平面,![]() 為
為![]() 的中點,
的中點,![]() ,四邊形
,四邊形![]() 為矩形,線段
為矩形,線段![]() 交
交![]() 于點
于點![]() .
.
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)在線段![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 與平面
與平面![]() 所成角的大小為
所成角的大小為![]() ?若存在,求出
?若存在,求出![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
【答案】(1)見解析(2)![]() (3)在線段
(3)在線段![]() 上存在一點
上存在一點![]() 滿足題意,且
滿足題意,且![]()
【解析】
(1)由題意結合線面平行的判定定理即可證得題中的結論;
(2)建立空間直角坐標系,利用兩個半平面的法向量可得二面角的余弦值,然后利用同角三角函數基本關系可得二面角的正弦值;
(3)假設點Q存在,利用直線的方向向量和平面的法向量計算可得點Q的存在性和位置.
(1)因為四邊形![]() 為矩形,所以
為矩形,所以![]() 為
為![]() 的中點.連接
的中點.連接![]() ,
,
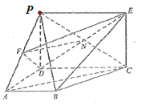
在![]() 中,
中,![]() 分別為
分別為![]() 的中點,所以
的中點,所以![]() ,
,
因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)易知![]() 兩兩垂直,如圖以
兩兩垂直,如圖以![]() 為原點,分別以
為原點,分別以![]() 所在直線為
所在直線為![]() 軸,建立空間直角坐標系.
軸,建立空間直角坐標系.
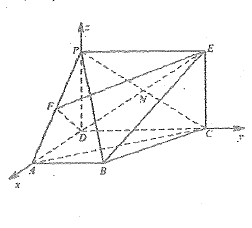
則![]() ,所以
,所以![]() .
.
設平面![]() 的法向量為
的法向量為![]() ,
,
則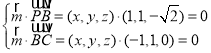 即
即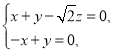 解得
解得
令![]() ,得
,得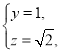
所以平面![]() 的一個法向量為
的一個法向量為![]() .
.
設平面![]() 的法向量為
的法向量為![]() ,
,
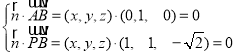 ,據此可得
,據此可得 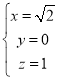 ,
,
則平面![]() 的一個法向量為
的一個法向量為![]() ,
,
![]() ,于是
,于是![]() .
.
故二面角![]() 的正弦值為
的正弦值為![]() .
.
(3)設存在點![]() 滿足條件.
滿足條件.
由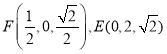 ,
,
設![]() ,整理得
,整理得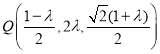 ,
,
則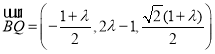 .
.
因為直線![]() 與平面
與平面![]() 所成角的大小為
所成角的大小為![]() ,
,
所以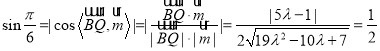
解得![]() ,
,
由![]() 知
知![]() ,即點
,即點![]() 與
與![]() 重合.
重合.
故在線段![]() 上存在一點
上存在一點![]() ,且
,且![]() .
.


 新活力總動員暑系列答案
新活力總動員暑系列答案 龍人圖書快樂假期暑假作業鄭州大學出版社系列答案
龍人圖書快樂假期暑假作業鄭州大學出版社系列答案科目:高中數學 來源: 題型:
【題目】教材中指出:當![]() 很小,
很小,![]() 不太大時,可以用
不太大時,可以用![]() 表示
表示![]() 的近似值,即
的近似值,即![]() (1),我們把近似值與實際值之差除以實際值的商的絕對值稱為“相對近似誤差”,一般用字母
(1),我們把近似值與實際值之差除以實際值的商的絕對值稱為“相對近似誤差”,一般用字母![]() 表示,即相對近似誤差
表示,即相對近似誤差![]()
(1)利用(1)求出![]() 的近似值,并指出其相對近似誤差(相對近似誤差保留兩位有效數字)
的近似值,并指出其相對近似誤差(相對近似誤差保留兩位有效數字)
(2)若利用(1)式計算![]() 的近似值產生的相對近似誤差不超過
的近似值產生的相對近似誤差不超過![]() ,求正實數
,求正實數![]() 的取值范圍;
的取值范圍;
(3)若利用(1)式計算![]() 的近似值產生的相對近似誤差不超過
的近似值產生的相對近似誤差不超過![]() ,求正整數
,求正整數![]() 的最大值。(參考對數數值:
的最大值。(參考對數數值:![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】朱世杰是歷史上最偉大的數學家之一,他所著的《四元玉鑒》卷中“如像招數”五問中有如下問題:今有官司差夫一千八百六十四人筑堤,只云初日差六十四人,次日轉多七人.”其大意為“官府陸續派遣1864人前往修筑堤壩,第一天派出64人,從第二天開始每天派出的人數比前一天多7人.”在該問題中的1864人全部派遣到位需要的天數為( )
A. 9B. 16C. 18D. 20
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,由半圓![]() 和部分拋物線
和部分拋物線![]() 合成的曲線
合成的曲線![]() 稱為“羽毛球開線”,曲線
稱為“羽毛球開線”,曲線![]() 與
與![]() 軸有
軸有![]() 兩個焦點,且經過點
兩個焦點,且經過點![]()

(1)求![]() 的值;
的值;
(2)設![]()
![]() 為曲線
為曲線![]() 上的動點,求
上的動點,求![]() 的最小值;
的最小值;
(3)過![]() 且斜率為
且斜率為![]() 的直線
的直線![]() 與“羽毛球形線”相交于點
與“羽毛球形線”相交于點![]() 三點,問是否存在實數
三點,問是否存在實數![]() 使得
使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由。
的值;若不存在,請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲袋中裝有3個白球和5個黑球,乙袋中裝有4個白球和6個黑球,現從甲袋中隨機取出一個球放入乙袋中,充分混合后,再從乙袋中隨機取出一個球放回甲袋中,則甲袋中白球沒有減少的概率為____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數![]() 在定義域內存在實數x,滿足
在定義域內存在實數x,滿足![]() ,則稱
,則稱![]() 為“局部奇函數”.
為“局部奇函數”.
![]() 已知函數
已知函數![]() ,試判斷
,試判斷![]() 是否為“局部奇函數”?并說明理由;
是否為“局部奇函數”?并說明理由;
![]() 設
設![]() 是定義在
是定義在![]() 上的“局部奇函數”,求實數m的取值范圍;
上的“局部奇函數”,求實數m的取值范圍;
![]() 若
若![]() 為定義域R上的“局部奇函數”,求實數m的取值范圍.
為定義域R上的“局部奇函數”,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對 n N ,設拋物線 y2 2(2n 1) x ,過 P 2n, 0 任作直線 l 與拋物線交與 An, Bn兩點,則數列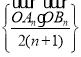 的前 n 項和為_____;
的前 n 項和為_____;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com