
【題目】下列四個圖形中,正方體棱上的四個中點共面的圖形是( ).

A.甲與乙B.乙與丙C.丙與丁D.丁與甲
【答案】A
【解析】
如圖所示:利用空間點線面位置關系可以證明圖中中點E、F、G、H、M、N六點共面,進而判斷甲乙圖中對應的四點為分別為:H、F、G、N和E、F、G、M均在平面EFGNMH內,所以可得甲乙圖形符合要求;然后可判斷丙和丁圖中對應的四點不共面.
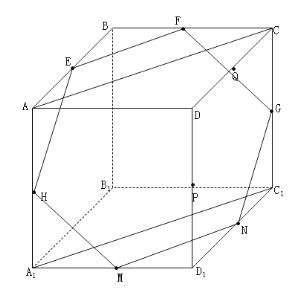
如圖所示, E、F、G、H、M、N、P、Q均為正方體AC1棱上的中點,所以有:EF![]() AC,MN
AC,MN![]() A1C1,AC
A1C1,AC![]() A1C1,得EF
A1C1,得EF![]() MN,所以得EF、MN可確定一個平面α,同理EH、NG可確定一個平面β,又因為E、F、M三點不共線只能確定一個平面,所以α、β重合,即E、F、G、H、M、N六點共面為平面EN,所以有:
MN,所以得EF、MN可確定一個平面α,同理EH、NG可確定一個平面β,又因為E、F、M三點不共線只能確定一個平面,所以α、β重合,即E、F、G、H、M、N六點共面為平面EN,所以有:
甲圖中對應的四點為H、F、G、N在平面EN內即共面;
乙圖中對應的四點為E、F、G、M在平面EN內即共面;
丙圖中對應的四點為E、F、P、M其中P點不在平面EN內即得四點不共面;
丁圖中對應的四點為E、H、G、Q其中Q點不在平面EN內即得四點不共面;
綜上可得甲乙圖滿足要求.
故選:A


科目:高中數學 來源: 題型:
【題目】已知非零復數![]() ,
,![]() ,
,![]() ;若
;若![]() ,
,![]() ,
,![]() 滿足
滿足![]() ,
,![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 所對應點
所對應點![]() 在圓
在圓![]() ,求
,求![]() 所對應的點的軌跡;
所對應的點的軌跡;
(3)是否存在這樣的直線![]() ,
,![]() 對應點在
對應點在![]() 上,
上,![]() 對應點也在直線
對應點也在直線![]() 上?若存在,求出所有這些直線;若不存在,若不存在,說明理由.
上?若存在,求出所有這些直線;若不存在,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的幾何體中,![]() 垂直于梯形
垂直于梯形![]() 所在的平面,
所在的平面,![]() 為
為![]() 的中點,
的中點,![]() ,四邊形
,四邊形![]() 為矩形,線段
為矩形,線段![]() 交
交![]() 于點
于點![]() .
.
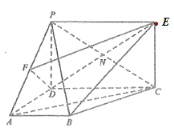
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)在線段![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 與平面
與平面![]() 所成角的大小為
所成角的大小為![]() ?若存在,求出
?若存在,求出![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,定義兩點![]() 與
與![]() 之間的“直角距離”為:
之間的“直角距離”為:![]() .現給出下列4個命題:
.現給出下列4個命題:
①已知![]() 、
、![]() ,則
,則![]() 為定值;
為定值;
②已知![]() 三點不共線,則必有
三點不共線,則必有![]() ;
;
③用![]() 表示
表示![]() 兩點之間的距離,則
兩點之間的距離,則![]() ;
;
④若![]() 是橢圓
是橢圓![]() 上的任意兩點,則
上的任意兩點,則![]() 的最大值為6.
的最大值為6.
則下列判斷正確的為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市為了解游客人數的變化規律,提高旅游服務質量,收集并整理了![]() 年
年![]() 月至
月至![]() 年
年![]() 月期間月接待游客量(單位:萬人)的數據,繪制了下面的折線圖.根據該折線圖,下列結論正確的是( )
月期間月接待游客量(單位:萬人)的數據,繪制了下面的折線圖.根據該折線圖,下列結論正確的是( )
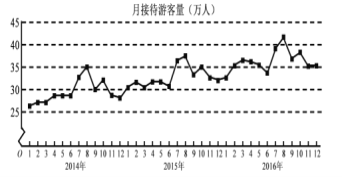
A. 月接待游客逐月增加
B. 年接待游客量逐年減少
C. 各年的月接待游客量高峰期大致在![]() 月
月
D. 各年![]() 月至
月至![]() 月的月接待游客量相對于
月的月接待游客量相對于![]() 月至
月至![]() 月,波動性較小,變化比較穩定
月,波動性較小,變化比較穩定
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com