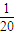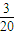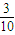一個袋中裝有6個形狀大小完全相同的小球,球的編號分別為1,2,3,4,5,6.
(Ⅰ)若從袋中每次隨機抽取1個球,有放回的抽取2次,求取出的兩個球編號之和為6的概率;
(Ⅱ)若從袋中每次隨機抽取2個球,有放回的抽取3次,求恰有2次抽到6號球的概率;
(Ⅲ)若一次從袋中隨機抽取3個球,記球的最大編號為X,求隨機變量X的分布列.
【答案】
分析:(Ⅰ)兩次取球的編號的一切可能結果(m,n)有6×6=36種,其中和為6的結果有共5種.
(Ⅱ)每次從袋中隨機抽取2個球,抽到編號為6的球的概率
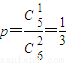
,故所求事件的概率為C
32p
2(1-p).
(Ⅲ)隨機變量X所有可能的取值為3,4,5,6,分別求出隨機變量X取每個值的概率,列表寫出分布列.
解答:解:(Ⅰ)設先后兩次從袋中取出球的編號為m,n,則兩次取球的編號的一切可能結果(m,n)有6×6=36種,
其中和為6的結果有(1,5),(5,1),(2,4),(4,2),(3,3),共5種,
則所求概率為
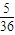
.
(Ⅱ)每次從袋中隨機抽取2個球,抽到編號為6的球的概率
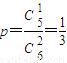
.
所以,3次抽取中,恰有2次抽到6號球的概率為
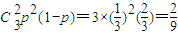
.
(Ⅲ)隨機變量X所有可能的取值為3,4,5,6,

,

,
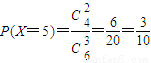
,
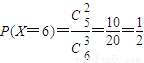
.
所以,隨機變量X的分布列為:
點評:本題考查求等可能事件的概率,求離散型隨機變量的分布列,求出隨機變量X所有可能的取值的概率,是解題的難點.

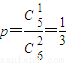 ,故所求事件的概率為C32p2(1-p).
,故所求事件的概率為C32p2(1-p).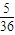 .
.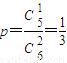 .
.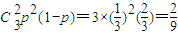 .
.  ,
, ,
,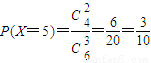 ,
,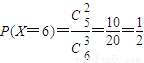 .
.