
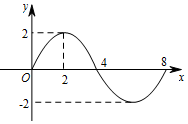
 函數y=Asin(ωx+φ)(A>0,ω>0)的部分圖象如示,則f(1)+f(2)+f(3)+…+f(210)的值等于( )
函數y=Asin(ωx+φ)(A>0,ω>0)的部分圖象如示,則f(1)+f(2)+f(3)+…+f(210)的值等于( )| A. | $\sqrt{2}$ | B. | $2+2\sqrt{2}$ | C. | $2+\sqrt{2}$ | D. | 0 |
分析 由函數的圖象的頂點坐標求出A,由周期求出ω,由五點法作圖求出φ的值,可得函數的解析式,再利用三角函數的周期性,求得所給式子的值.
解答 解:根據函數y=Asin(ωx+φ)(A>0,ω>0)的部分圖象,
可得A=2,$\frac{1}{2}•\frac{2π}{ω}$=8-4,∴ω=$\frac{π}{4}$,
∴函數的解析式為y=2sin($\frac{π}{4}$x+φ),
再根據五點法作圖可得$\frac{π}{4}•0$+φ=0,∴函數的解析式為y=2sin$\frac{π}{4}$x,
故函數的周期為$\frac{2π}{\frac{π}{4}}$=8,
f(1)+f(2)+f(3)+…+f(8)=$\sqrt{2}$+2+$\sqrt{2}$+0+(-$\sqrt{2}$)+(-2)+(-$\sqrt{2}$)+0=0,
∴f(1)+f(2)+f(3)+…+f(210)=f(1)+f(2)+f(3)+…+f(1024)
=128•[f(1)+f(2)+f(3)+…+f(8)]=0,
故選:D.
點評 本題主要考查由函數y=Asin(ωx+φ)的部分圖象求解析式,由函數的圖象的頂點坐標求出A,由周期求出ω,由五點法作圖求出φ的值,三角函數的周期性的應用,屬于中檔題.


 世紀百通主體課堂小學課時同步達標系列答案
世紀百通主體課堂小學課時同步達標系列答案 世紀百通優練測系列答案
世紀百通優練測系列答案 百分學生作業本題練王系列答案
百分學生作業本題練王系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
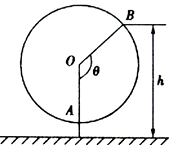 如圖是一個纜車示意圖,該纜車的半徑為4.8m,圓上最低點與地面的距離為0.8m,纜車每60s轉動一圈,圖中OA與地面垂直,以OA為始邊,逆時針轉動θ角到OB,設B點與地面的距離為hm.
如圖是一個纜車示意圖,該纜車的半徑為4.8m,圓上最低點與地面的距離為0.8m,纜車每60s轉動一圈,圖中OA與地面垂直,以OA為始邊,逆時針轉動θ角到OB,設B點與地面的距離為hm.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com