【題目】2010-2018年之間，受益于基礎設施建設對光纖產品的需求，以及個人計算機及智能手機的下一代規格升級，電動汽車及物聯網等新機遇，連接器行業增長呈現加速狀態．根據該折線圖，下列結論正確的個數為（ ）
①每年市場規模量逐年增加；
②增長最快的一年為2013～2014；
③這8年的增長率約為40％；
④2014年至2018年每年的市場規模相對于2010年至2014年每年的市場規模，數據方差更小，變化比較平穩
A. 1B. 2C. 3D. 4
科目：高中數學 來源： 題型：
【題目】用0與1兩個數字隨機填入如圖所示的5個格子里，每個格子填一個數字，并且從左到右數，不管數到哪個格子，總是1的個數不少于0的個數，則這樣填法的概率為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
為橢圓E： 
的左、右頂點， 
，E的兩個焦點與E的短軸兩個端點所構成的四邊形是正方形．
（1）求橢圓E的方程；
（2）設動點
（
），記直線
與E的交點（不同于
）到x軸的距離分別為
，求
的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平行四邊形OABC中，過點C的直線與線段OA、OB分別相交于點M、N，若
，
；（1）求y關于x的函數解析式；（2）定義函數
，點列Pi（xi，F（xi））（i=1，2，…，n，n≥2）在函數y=F（x）的圖象上，且數列{xn}是以1為首項，0.5為公比的等比數列，O為原點，令
，是否存在點Q（1，m），使得
？若存在，求出Q點的坐標，若不存在，說明理由；
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知直線
的參數方程為
（
為參數），以坐標原點為極點， 
軸的非負半軸為極軸建立極坐標系，圓
的極坐標方程為
，直線
與圓
交于
， 
兩點.
（1）求圓
的直角坐標方程及弦
的長；
（2）動點
在圓
上（不與
， 
重合），試求
的面積的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若一個函數當自變量在不同范圍內取值時，函數表達式不同，我們稱這樣的函數為分段函數．下面我們參照學習函數的過程與方法，探究分段函數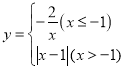
的圖象與性質．列表：
x | … |
|
|
|
|
|
| 0 |
| 1 |
| 2 |
| 3 | … |
y | … |
|
| 1 |
| 2 |
| 1 |
| 0 |
| 1 |
| 2 | … |
描點：在平面直角坐標系中，以自變量x的取值為橫坐標，以相應的函數值y為縱坐標，描出相應的點，如圖所示．
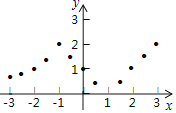
（1）如圖，在平面直角坐標系中，觀察描出的這些點的分布，作出函數圖象；
（2）研究函數并結合圖象與表格，回答下列問題：
①點
，
，
，
在函數圖象上，
，
；（填“＞”，“＝”或“＜”）
②當函數值
時，求自變量x的值；
③在直線
的右側的函數圖象上有兩個不同的點
，
，且
，求
的值；
④若直線
與函數圖象有三個不同的交點，求a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知下列命題：
①在某項測量中，測量結果
服從正態分布
，若在
內取值范圍概率為
，則在
內取值的概率為
；
②若
，
為實數，則“
”是“
”的充分而不必要條件；
③已知命題
，
，則
是：
，
；
④
中，“角
，
，
成等差數列”是“
”的充分不必要條件；其中，所有真命題的個數是（ ）
A. 
個 B. 
個 C. 
個 D. 
個
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】定義在R上的偶函數f(x)滿足f(x＋1)＝－f(x)且f(x)在[－1,0]上是增函數，給出下列四個命題：
①f(x)是周期函數；②f(x)的圖象關于x＝1對稱；③f(x)在[1,2]上是減函數；④f(2)＝f(0)．
其中正確命題的序號是____________．(請把正確命題的序號全部寫出來)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
