
【題目】某企業為確定下一年投入某種產品的研發費用,需了解年研發費用![]() (單位:千萬元)對年銷售量
(單位:千萬元)對年銷售量![]() (單位:千萬件)的影響,統計了近10年投入的年研發費用
(單位:千萬件)的影響,統計了近10年投入的年研發費用![]() 與年銷售量
與年銷售量![]() 的數據,得到散點圖如圖所示.
的數據,得到散點圖如圖所示.

(1)利用散點圖判斷![]() 和
和![]() (其中
(其中![]() 均為大于0的常數)哪一個更適合作為年銷售量
均為大于0的常數)哪一個更適合作為年銷售量![]() 和年研發費用
和年研發費用![]() 的回歸方程類型(只要給出判斷即可,不必說明理由);
的回歸方程類型(只要給出判斷即可,不必說明理由);
(2)對數據作出如下處理,令![]() ,得到相關統計量的值如表:根據第(1)問的判斷結果及表中數據,求
,得到相關統計量的值如表:根據第(1)問的判斷結果及表中數據,求![]() 關于
關于![]() 的回歸方程;
的回歸方程;
|
|
|
|
15 | 15 | 28.25 | 56.5 |
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為 .
.
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線![]() 在平面直角坐標系
在平面直角坐標系![]() 下的參數方程為
下的參數方程為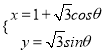 (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系.
軸正半軸為極軸,建立極坐標系.
(1)求曲線![]() 的普通方程及極坐標方程;
的普通方程及極坐標方程;
(2)直線![]() 的極坐標方程是
的極坐標方程是![]() ,射線
,射線![]() :
: ![]() 與曲線
與曲線![]() 交于點
交于點![]() 與直線
與直線![]() 交于點
交于點![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】二手經銷商小王對其所經營的![]() 型號二手汽車的使用年數
型號二手汽車的使用年數![]() 與銷售價格
與銷售價格![]() (單位:萬元/輛)進行整理,得到如下數據:
(單位:萬元/輛)進行整理,得到如下數據:

下面是![]() 關于
關于![]() 的折線圖:
的折線圖:
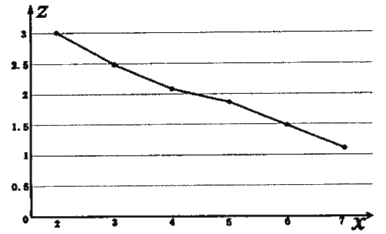
(1)由折線圖可以看出,可以用線性回歸模型擬合![]() 與
與![]() 的關系,請用相關系數加以說明;
的關系,請用相關系數加以說明;
(2)求![]() 關于
關于![]() 的回歸方程并預測某輛
的回歸方程并預測某輛![]() 型號二手汽車當使用年數為9年時售價大約為多少?(
型號二手汽車當使用年數為9年時售價大約為多少?(![]() 、
、![]() 小數點后保留兩位有效數字).
小數點后保留兩位有效數字).
(3)基于成本的考慮,該型號二手車的售價不得低于7118元,請根據(2)求出的回歸方程預測在收購該型號二手車時車輛的使用年數不得超過多少年?
參考公式:回歸方程![]() 中斜率和截距的最小二乘估計公式分別為:
中斜率和截距的最小二乘估計公式分別為:
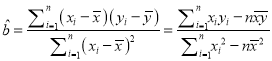 ,
,![]() .
. 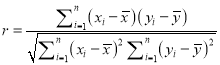 .
.
參考數據:
![]() ,
,![]() ,
,![]() ,
,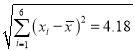 ,
,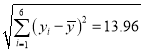 ,
,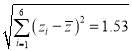 ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為弘揚傳統文化,某校舉行詩詞大賽.經過層層選拔,最終甲乙兩人進入總決賽,爭奪冠軍.決賽規則如下:①比賽共設有五道題;②雙方輪流答題,每次回答一道,兩人答題的先后順序通過抽簽決定;③若答對,自己得1分;若答錯,則對方得1分;④先得3分者獲勝.已知甲、乙答對每道題的概率分別為![]() 和
和![]() ,且每次答題的結果相互獨立.
,且每次答題的結果相互獨立.
(Ⅰ)若乙先答題,求甲3:0獲勝的概率;
(Ⅱ)若甲先答題,記乙所得分數為![]() ,求
,求![]() 的分布列和數學期望
的分布列和數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種汽車購買時費用為14.4萬元,每年應交付保險費、養路費及汽油費共0.9萬元,汽車的維修費為:第一年0.2萬元,第二年0.4萬元,第三年0.6萬元,……,依等差數列逐年遞增.
(Ⅰ)設使用n年該車的總費用(包括購車費用)為f(n),試寫出f(n)的表達式;
(Ⅱ)求這種汽車使用多少年報廢最合算(即該車使用多少年平均費用最少).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() ,直線
,直線![]() 交
交![]() 于
于![]() 兩點,
兩點, ![]() 是
是![]() 的中點,過
的中點,過![]() 作
作![]() 軸的垂線交
軸的垂線交![]() 于
于![]() 點.
點.

(1)證明:拋物線![]() 在
在![]() 點處的切線與
點處的切線與![]() 平行;
平行;
(2)是否存在實數![]() ,使以
,使以![]() 為直徑的圓
為直徑的圓![]() 經過
經過![]() 點?若存在,求出
點?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點
的兩個焦點![]() ,
,![]() ,離心率為
,離心率為![]() ,
,![]() 的周長等于
的周長等于![]() ,點
,點![]() 、
、![]() 在橢圓上,且
在橢圓上,且![]() 在
在![]() 邊上.
邊上.

(1)求橢圓![]() 的標準方程;
的標準方程;
(2)如圖,過圓![]() 上任意一點
上任意一點![]() 作橢圓的兩條切線
作橢圓的兩條切線![]() 和
和![]() 與圓
與圓![]() 交與點
交與點![]() 、
、![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com